2021-12-25
207
IV. С помощью интеграла Мора определим прогиб балки посередине между опорами.
Для определения прогиба балки посередине между опорами используем интеграл Мора:
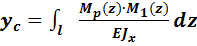
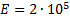МПа
Для швеллера №20а:
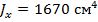
В интересующей нас точке сечения С приложим единичную силу.
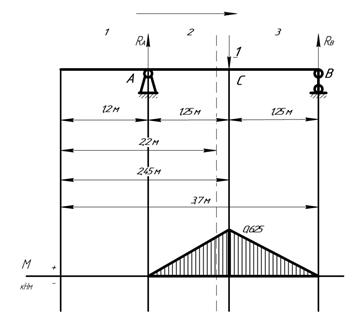Сначала определим опорные реакции (в т.А – неподвижный шарнир, в т.В – подвижный):
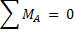
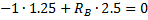
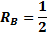
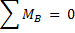
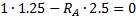
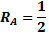
Выполняем проверку правильности нахождения реакций. для этого составляем дополнительно уравнение равновесия, проектируя силы на вертикальную ось:
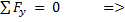
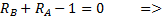
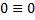
Следовательно, значения реакций найдены верно.
На схеме балки можно выделить 3 разных участка. Записываем уравнение изгибающих моментов для каждого участка (движемся слева направо):
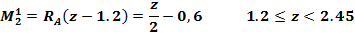
z=1.2 м,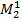 
=0 м z=2.45 м, 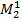=0.625 м
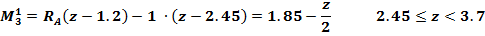
z=2.45 м,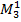 
=0.625 м z=3.7 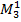м, =0 м
Определим прогиб балки посередине между опорами(единичная силы направлена против прогиба):
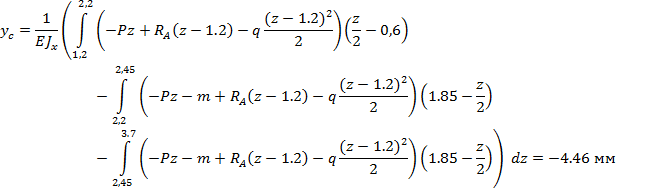
V. Проверим выполнение условия жесткости.
Определим допускаемый прогиб:
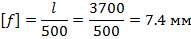
Максимальный прогиб для 1 участка: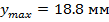 
Т.к.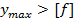 
, делаем вывод, что условие жёсткости не выполняется.
Максимальный прогиб между опорами: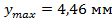 
Т.к.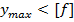 
, делаем вывод, что условие жёсткости выполняется.
