2023-09-19
395
Теорема Кастильяно
Частная производная от дополнительной потенциальной энергии деформаций по обобщённой силе равна обобщённому перемещению.
,
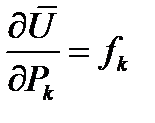где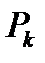 
обобщённая сила, а 
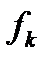обобщённое перемещение. В качестве обобщённой силы понимаем просто силу, а также момент, в первом случае определяем линейное перемещение, а во втором угловое перемещение k-го узла или сечения.
Применение принципа Лагранжа в теории изгиба балок
Получим дифференциальное уравнение изгиба балки и статические граничные условия, используя принцип Лагранжа. Потенциальная энергия изгиба балки на основании формул (4.8) будет
.
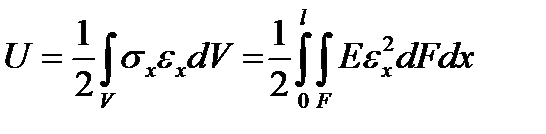На основании гипотезы «плоских сечений»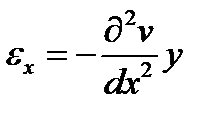 
, где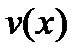 
- прогиб балки в направлении оси у, тогда
.
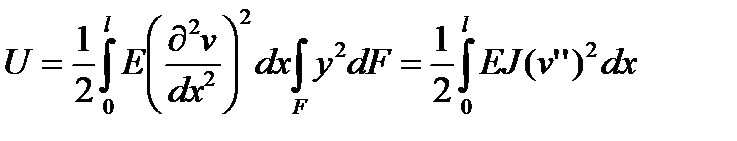Работа внешней нагрузки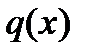 
.
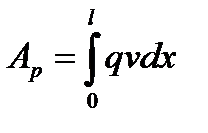Полная энергия балки
.
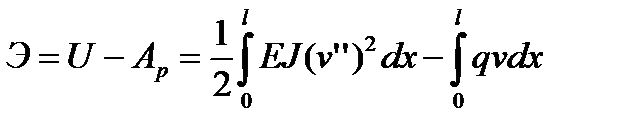Уравнение Лагранжа
.
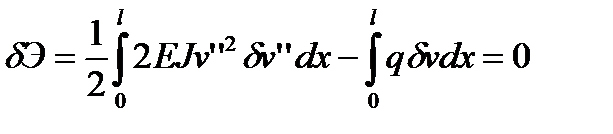Интегрируя первый интеграл дважды по частям и учитывая перестановочность операций варьирования и дифференцирования: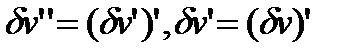 
, получим
.
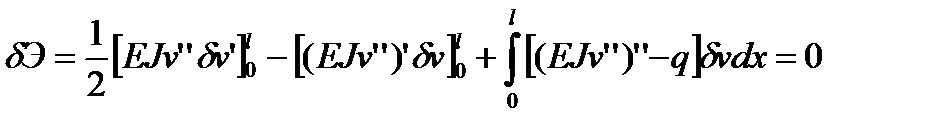Если заданы кинематические граничные условия
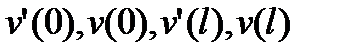, то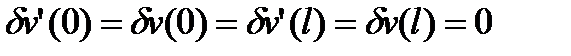 
|
|
|
и внеинтегральные члены исчезает, а интеграл равен нулю при произвольной вариации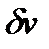 
на участке 
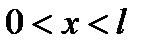только тогда, когда нулю равно подынтегральное выражение, т.е.
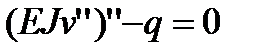. 1
Это есть дифференциальное уравнение Эйлера, которое в данной задаче представляет уравнение изогнутой оси балки и является уравнением равновесия в перемещениях.
Если же кинематические граничные условия не заданы (например, для свободной балки), то 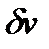и 
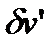произвольны всюду, включая точк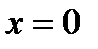и 
и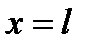 
, поэтому вариационное уравнение будет удовлетворено только в том случае, если выполняется (1) и естественные граничные условия 
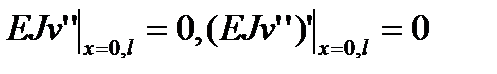, которые являются статическими граничными условиями для свободной балки.
Таким образом, при любых комбинациях заданных кинематических граничных условий получаем уравнение изгиба балки (1) и соответствующие естественные статические граничные условия.
