Постановку задачи в перемещениях или напряжениях можно осуществить используя вариационные формулы соответственно Лагранжа или Кастильяно. Введём понятие полной энергии деформируемого тела, состящей из потенциальной энергии деормаций и работы внешних сил. Обозначим полную энергию деформируемого тела через Э, а потенциалную энергию деформаций через U.
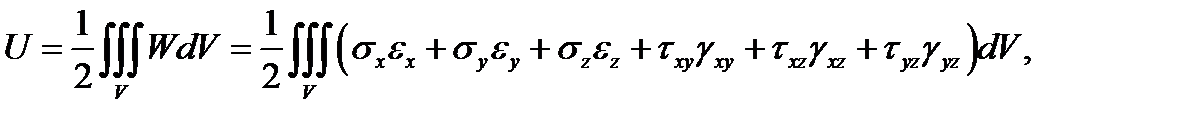 (4.5)
(4.5)
где V и dV объём и элеменарный объём деформируемого тела соответственно.
Работа внешних объёмных и поверхностных сил A определяется формулой
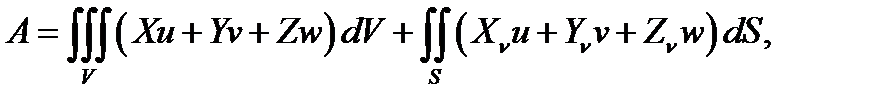 (4.6)
(4.6)
где X , Y , Z составляющие объёмной, а 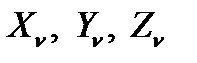 составляющие поверхностной нагрузки. Здесь и далее перед составляющими объёмной нагрузки опускаем удельную плотность
составляющие поверхностной нагрузки. Здесь и далее перед составляющими объёмной нагрузки опускаем удельную плотность 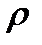 , считая , что объёмные силы задаются с размерностью [
, считая , что объёмные силы задаются с размерностью [ 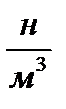 ].
].
Соответственно, первый интеграл приведённой формулы берётся по всему объёму тела, а второй интеграл – по всей его поверхности, в первом подинтегральном выражении u , v , w упругие перемещения вдоль осей координат x , y , z соответственно, а во втором интеграле те же перемещения, но имеющие место на поверхности деформируемого тела.
Полная энергия деформируемого тела
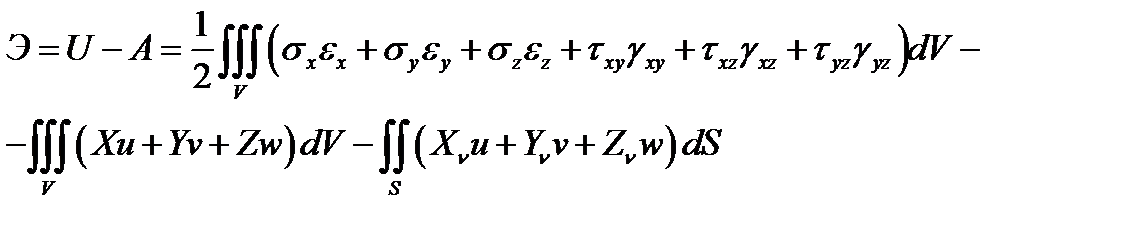 (4.7)
(4.7)
Знак минус в этом выражении объясняется тем, что работы внутренних и внешних сил являются разнонаправленными.
Потенциальная энергия деформаций и, сосответственено, полная энергия деформируемого тела могут быть записаны через перемещения, если в этих формулах исключить напряжения с помощью физических соотношений (3.1), (3.5) и (3.9) для анизотропного, ортотропного или изотропного материалов, а деформации выразить через перемещения с помощью соотношений Коши (2.1). Также можно удельную энергию деформаций и полную энергию тела представить в напряжениях исключив деформации с помощью физических соотношений (3.2), (3.10) и (3.11) для анизотропного, ортотропного и изотропного материалов соответственно. Форма записи полной энергии, представленная формулой (4.7) является смешанной.
Если деформациям, а значит и перемещениям дать малые приращения, то приращение полной нергии тела запишем в виде
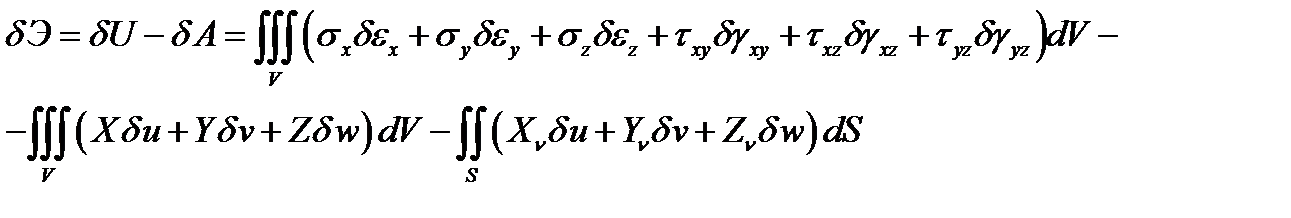 (4.8) Здесь знак
(4.8) Здесь знак 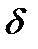 является знаком первой вариации, а записанное выражение иллюстрирует начало изменений деформированного состояния. Следует отметить, что напряжения при этом не варьируются, что полная энергия тела является функционалом, так как зависит не только от координат, но и от функций и их производных
является знаком первой вариации, а записанное выражение иллюстрирует начало изменений деформированного состояния. Следует отметить, что напряжения при этом не варьируются, что полная энергия тела является функционалом, так как зависит не только от координат, но и от функций и их производных
Принцип Лагранжа: из всех возможых систем перемещений действительные перемещения сообщают полной энергии тела стационарное (минимальное) значение, тогда
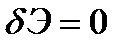 (4.9)
(4.9)
Эта математическая запись принипа Лагранжа, по сути, есть условие экстремума функционала полной энергии, поэтому о его максимуме или минимуме можно определённо говорить только после определения знака второй вариации функционала энергии. Для большинства задач механики деформируемого твёрдого тела 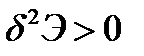 , поэтому можно без ошибки утверждать, что условие (4.9) есть условие минимума полной энергии тела. Необходимо отметить, что возможные перемещения должны удовлетворять всем кинематическим связям, наложенным на деформируемое тело, это соотношения Коши (2.1) и кинематические условмя на поверхности тела.
, поэтому можно без ошибки утверждать, что условие (4.9) есть условие минимума полной энергии тела. Необходимо отметить, что возможные перемещения должны удовлетворять всем кинематическим связям, наложенным на деформируемое тело, это соотношения Коши (2.1) и кинематические условмя на поверхности тела.
Результатом применения вариационной формулы Лагранжа (4.9) будет получение уравнений равновесия и статических граничных условий. Покажем это на примере небольшого фрагмента общей формулы, в котором деформации выражены через перемещения с помощью соотношений (2.1)
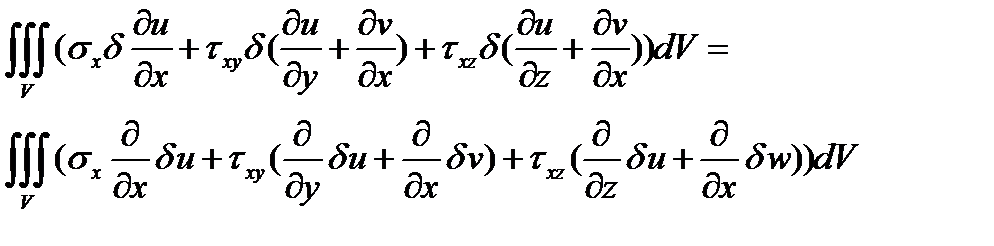
Отбросим вторые члены в скобках после касательных напряжений и, проинтегрировав полученное по частям будем иметь
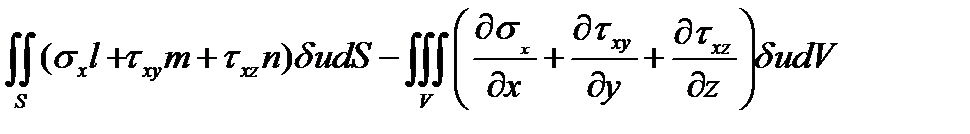
Добавляя кэтому выражению работу объёмных и поверхностных сил, действующих в направлении оси x , получим выражение
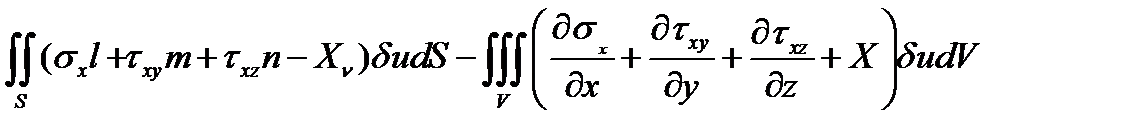 .
.
Производя аналогичные операции с вариацией полного функционала
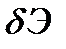 , получим
, получим
Поскольку вариации перемещений в объёме и на поверхности тела являются независимыми, то для выполнения этого условия необходимо приравнять нулю выражения в скобках, стоящие при вариациях перемещений. В результате получим уравнения равновесия и статические граничные условия, что и требовалось доказать.
Если в выражении (4.8) исключить напряжения с помощью физических соотношений для изотропного материала, а деформации с помощью соотношений Коши (2.1), получим  в перемещениях
в перемещениях

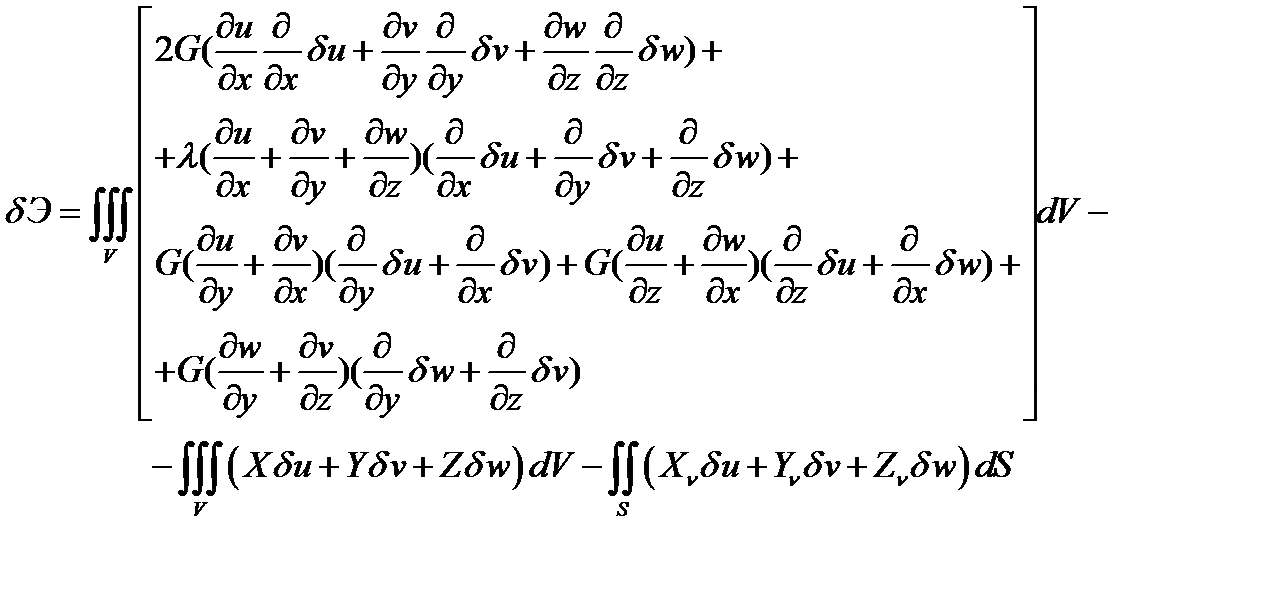
Приравнивая это выражение нулю и выполняя интегрирование по частям, получим уравнения равновесия в перемещениях (4.3) и естественные граничные условия, которые записываются в виде работы сил на возможных перемещениях. Таким образом, формула Лагранжа представляет собой вариационную постановку задачи теории упругости в перемещениях.
Рассмотрим вариационную постановку задачи теории упругости в напряжениях. В этом случае варьируются напряжения, а деформации и перемещения не варьируются. Первую вариацию полной энергии тела запишем в виде
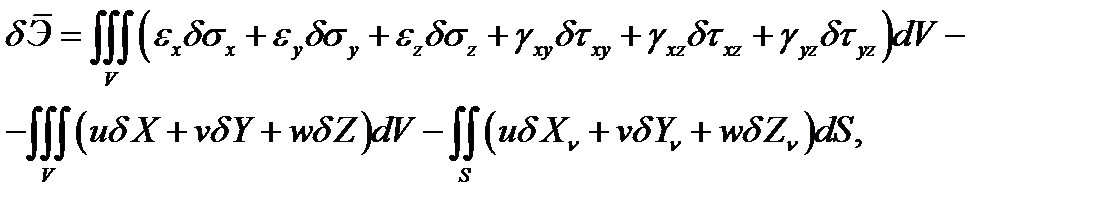 (4.10)
(4.10)
где 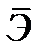 --полная дополнительная энергия тела, первый интеграл в этом выражении есть вариация дополнительной потениальной энергии деформаций
--полная дополнительная энергия тела, первый интеграл в этом выражении есть вариация дополнительной потениальной энергии деформаций 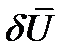 , второй и третий интегралы представляют собой вариацию работы внешних объёмных и поверхностных сил. В силу того, что объёмные силы всегда известны, они не варьируются, вследствие чего второй интеграл в (4.10) следует отбросить.
, второй и третий интегралы представляют собой вариацию работы внешних объёмных и поверхностных сил. В силу того, что объёмные силы всегда известны, они не варьируются, вследствие чего второй интеграл в (4.10) следует отбросить.
Для линейно упругих тел 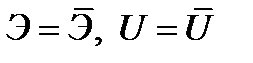 , но для нелинейно упругого материала эти равенства не выполняются, и это учитывается в названиях введением терминов «дополнительная энергия» и «дополнительная работа».
, но для нелинейно упругого материала эти равенства не выполняются, и это учитывается в названиях введением терминов «дополнительная энергия» и «дополнительная работа».
Принцип Кастильяно: из всех статически возможных систем напряжений истинные напряжения сообщают полной дополнительной энергии тела стационарное (минимальное значение). В соорветствии с этим принципом имеем вариационную формулу Кастильяно
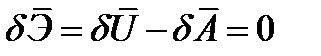 , (4.11)
, (4.11)
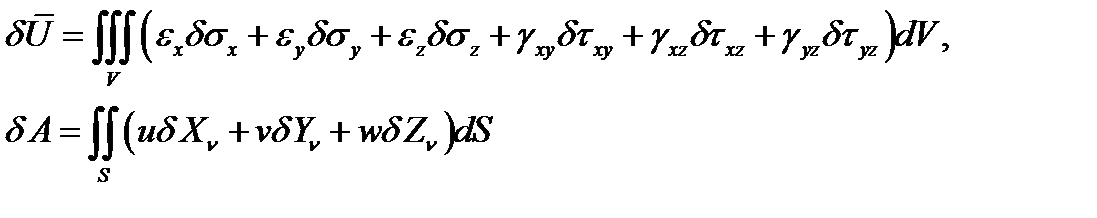
Статически возможными напряжениями являются те, которые удовлетворяют уравнениям равновесия в объёме (1.4) и на поверхности тела (1.6). Если поверхностные силы заданы, то их вариации равны нулю, и тогда получим вариационную формулу принцпа наменьшей работы, являющегося частным случаем принципа Кастильяно
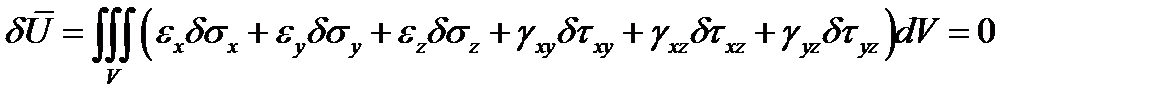 (4.12)
(4.12)
Формулируется принип наименьшей работы так же как и принцип Кастильяно с той лишь разницей, что полную дополнительную энергию в формулировке следует заменить дополнительной потенциальной энергией деформации.
Выразим шесть напряжений 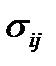 через шесть функций
через шесть функций 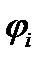 так, чтобы уравнения равновесия (1.4) были удовлетворены
так, чтобы уравнения равновесия (1.4) были удовлетворены
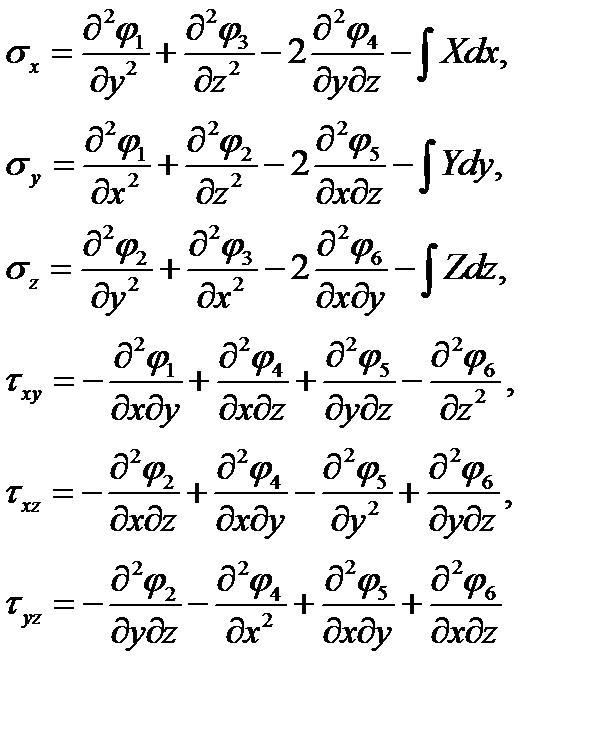 (4.13)
(4.13)
и подставим в (4.12)
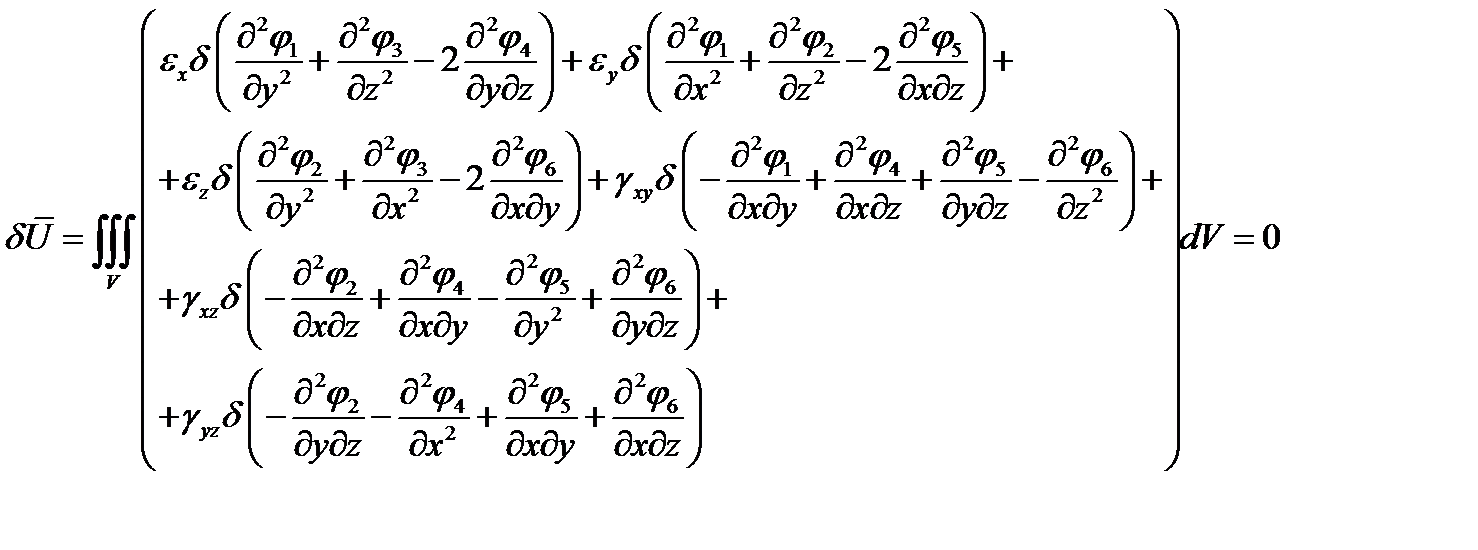
Выделим отдельно фрагмент этой формулы, содержащий только члены при производных от функции 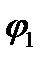
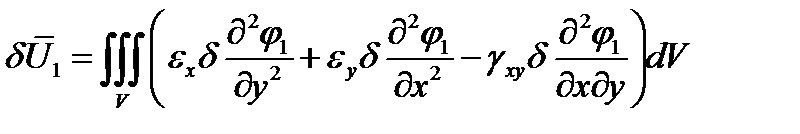 .
.
После интегрирования по частям получим ряд поверхностных интегралов, содержащих функцию 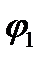 и её производные, которыми без ущерба для задачи ввиду малости можно пренебречь, и объёмный интеграл в виде
и её производные, которыми без ущерба для задачи ввиду малости можно пренебречь, и объёмный интеграл в виде
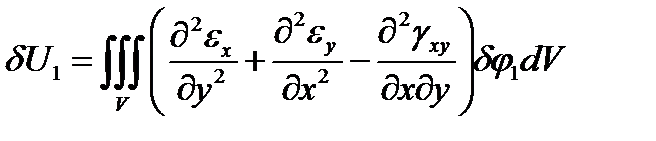 .
.
При вариациях других функций 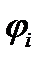 получим аналогичные выражения, а поскольку вариации этих функций проивольны и независимы, то подинтегальные выражения в скобках небходимо приравнять нулю для выполнения условия (4.12). Таким образом, получим шесть уравнений совместности деформаций Сен-Венана. Если деормации в (4.12) исключить с помощью физических соотношений, то в резльтате применения вариационной формулы Кастильяно получим уравнения совместности в напряжениях.
получим аналогичные выражения, а поскольку вариации этих функций проивольны и независимы, то подинтегальные выражения в скобках небходимо приравнять нулю для выполнения условия (4.12). Таким образом, получим шесть уравнений совместности деформаций Сен-Венана. Если деормации в (4.12) исключить с помощью физических соотношений, то в резльтате применения вариационной формулы Кастильяно получим уравнения совместности в напряжениях.
В заключение приведём формулы для определения дополнительной потенциальной энергии деформаций стержневых систем, которые в дальнейшем нам понадобятся.
Для изолированного ферменного стержня, работающего только на растяжение или сжатие, в равенстве (4.5) в подинтегральном выражении останется только первое слагаемое. Исключив деформацию с помощью закона Гука для изотропного материала 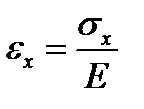 , получим потенциальную энергию деформаций изолированного стержня в напряжениях. Далее, интегрируя по площади поперечного сечения, окончательно запишем
, получим потенциальную энергию деформаций изолированного стержня в напряжениях. Далее, интегрируя по площади поперечного сечения, окончательно запишем

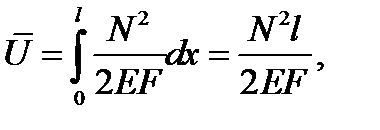
Где 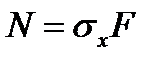 , l – длина стержня, F – площадь поперечного сечения стержня.
, l – длина стержня, F – площадь поперечного сечения стержня.
Если стержень нагревается, то закон Гука записывается с учётом температурного воздействия 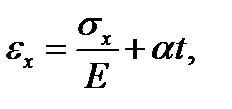 где второе слагаемое представляет произведение коэффициента линейного расширения на температуру нагрева стержня. Тогда дополнительная потенциальная энергия деформаций имеет вид
где второе слагаемое представляет произведение коэффициента линейного расширения на температуру нагрева стержня. Тогда дополнительная потенциальная энергия деформаций имеет вид
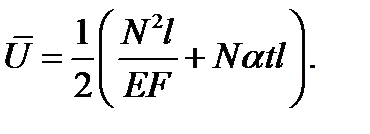

Для ферменной системы, состоящей из n стержней
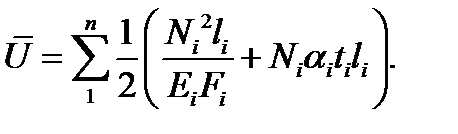
Во втором слагаемом в скобках учитываются только нагреваемые стержни.
Для изолированной балки (балочного элемента), работающей, в основном, на изгиб, для получения необходимой формулы воспользуемся общим выражением (4.5), оставляя в нём только первое слагаемое, как и для изолированного ферменного элемента. Исключая деформацию с помощью закона Гука для одноосного напряжённого состояния без учёта нагрева и перходя от напряжения к изгибающему моменту по формуле 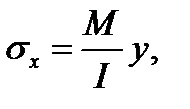 получим
получим

где M – изгибающий момент в поперечном сечении балки, I – момент инерции поперечного сечения.
Для системы n балочных элементов
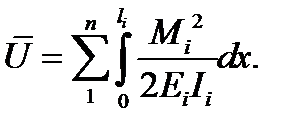
Для комбинированной системы, состоящей из m ферменных и n балочных элементов
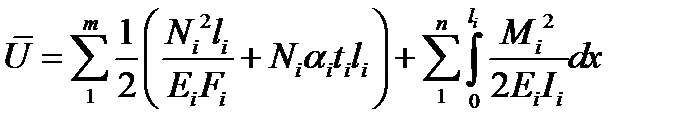 .
.
 2023-09-19
2023-09-19 1461
1461







