Метод Ньютона

Рассмотрим методы второго порядка с использованием вторых производных .

Все они являются обобщением метода Ньютона для отыскания корня уравнения.

                                                                                                     (1)

Разложим   в ряд около

                                           (2)

В результате получим алгоритм

                                                                                  (3)

Процесс (3) еще называется методом касательных для поиска корня уравнения (1).

Пусть теперь  является градиентом функции  

Приравнивая её к нулю и используя (3) получим

                                                                (4)

Процесс (4) сходится к некоторой стационарной точке

Если матрица  положительно определена, то  - точка min .

Нетрудно видеть, что метод Ньютона можно интерпретировать как поиск min квадратичных аппроксимирующих функций.

Этот метод гораздо эффективней, чем градиент методы.

Причем в данном методе не надо выбирать шаг 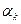. Он равен 1. то есть

Но на сходимость этого метода можно рассчитывать лишь в том случае, когда  матрица Гессе хорошо обусловлена и положительно определена, и если функция  является сильно выпуклой.

Рассмотрим пример, когда метод не работает.

Пусть

Если , то приходим к расходящемуся процессу. То есть метод Ньютона сильно зависит от выбора начальной точки . Если  находится в ближайшей окрестности , и функция  - квадратично аппроксимируема, то быстро сходится.

В связи с этим рассмотрим алгоритмы с регулировкой шага (Метод Ньютона - Рафсона).

                                                             (5)

Для выбора  используется метод дробления шага. То есть проверка неравенства

                                    (6).

.

Другой метод - определения шага 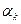 из задачи 

                                                             (7)