2021-08-14
360
Метод наискорейшего спуска.
Более эффективными являются методы, когда на каждой итерации шаг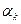 
выбирается из условия:
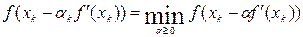(8)
- Метод наискорейшего спуска
Но в них на каждом шаге приходится решать задачу min (8).
Доказательство теоремы о сходимости данного алгоритма
Эффект оврагов.
Градиентные методы сходятся со скоростью геометрической прогрессии и если матрица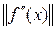 
хорошо обусловлена, то сходимость высокая, но в случае плохой обусловленности – после этой матрицы приходим к эффекту оврагов.
Пример:
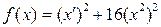
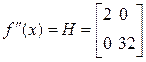
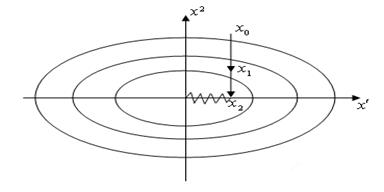
Быстрая сходимость по переменной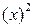 
(Спуск в овраг) и медленная сходимость по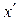 
Выход
1. Изменение масштабов переменных т.е. приведение к круговой форме
2. Эвристические схемы
а) Пусть в точке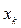 
вычислены 
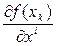- частная производная
Задаём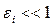 
и полагаем 
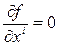, если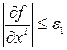 
т.е. производим быстрый спуск на дно.
б) Задаём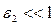 
и полагаем 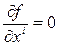, если 
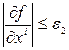, т.е. идём по берегу оврага, вдоль его дна.
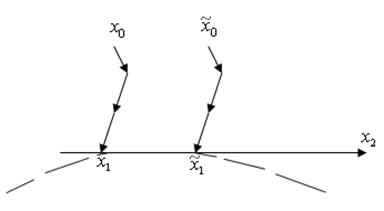
3. Метод оврагов (Гельфанд)
Пусть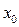 
и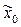 
- две близкие точки. Из этих точек производим спуск 
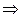получаем точк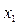и 
и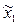 
, которые лежат в окрестности «дна оврага». Соединяя их прямой, делаем большой шаг 
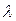в полученном направлении получаем точку 
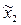и повторяем процедуру
Метод покоординатного спуска
Стремление уменьшить объем вычислительной работы на одной итерации приводит к упрощению градиентного метода.
Пусть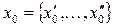 
- приближение.
Вычислим частную производную по первой координате и примем
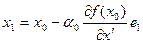, где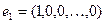 
- единичный орт оси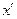 
Следующая итерация – вычисляют точку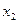 
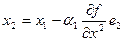и т.д.
Спуск по всем n – координатам составляет одну внешнюю итерацию. 
