1. Градиентные методы (методы первого порядка).
Как мы знаем, градиент  в точке
в точке  направлен в сторону наибольшего возрастания функции и ортогонален линии уровня в точке
направлен в сторону наибольшего возрастания функции и ортогонален линии уровня в точке  .
.
Вектор  - антиградиент, направлен в сторону наибольшего убывания
- антиградиент, направлен в сторону наибольшего убывания  .
.
Выберем в качестве направления  антиградиент
антиградиент  в точке
в точке  и придем к алгоритму:
и придем к алгоритму:
 (5)
(5)
в координатной форме
 (6)
(6)
Методы (5) и (6) называют градиентными методами, и они отличаются друг от друга способами выбора шага 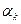 . Таких способов существует много, но наиболее распространены 2:
. Таких способов существует много, но наиболее распространены 2:
1. Метод с дроблением шага, связан с проверкой на каждой итерации некоторого неравенства.
2. Метод, в котором при переходе от  к
к  функция
функция  - метод наискорейшего спуска.
- метод наискорейшего спуска.
Метод с дроблением шага.
Рассмотрим процесс (5). Как выбрать шаг 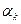 ? Малый шаг
? Малый шаг 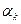 обеспечит убывание функции
обеспечит убывание функции

Но приводит к большому числу операций. Но большой шаг 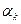 может вызвать неожиданно большой рост функции, либо приводит к колебаниям(цикл).
может вызвать неожиданно большой рост функции, либо приводит к колебаниям(цикл).
Рассмотрим пример:

 ,
, 

При  - процесс сходится
- процесс сходится
При  - процесс расходится
- процесс расходится
При  , то
, то  ,
,  ,
,  - процесс зацикливается.
- процесс зацикливается.
В методах с дроблением шага 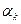 выбирается так, чтобы выполнялось неравенство
выбирается так, чтобы выполнялось неравенство
 , (7)
, (7)
где  , т.е. функция должна убывать на каждом шаге.
, т.е. функция должна убывать на каждом шаге.
Делают так: выбирают  и на k-й итерации проверяют выполнение (7). Если оно выполняется, то
и на k-й итерации проверяют выполнение (7). Если оно выполняется, то  . Если нет, то шаг
. Если нет, то шаг 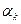 дробят до тех пор пока оно не выполнится.
дробят до тех пор пока оно не выполнится.
Процесс выглядит так:

Ломанная  ,
,  ,
, 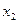 … аппроксимирует градиентную кривую.
… аппроксимирует градиентную кривую.
Процедура проверки (7) является достаточно трудоёмкой, поэтому используют другую информацию. Например
 ,
,
тогда можно взять 
 2021-08-14
2021-08-14 159
159








