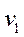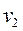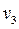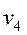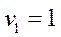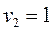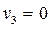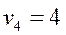Задача 1. Найти оптимальный план транспортной задачи

Найти оптимальный план транспортной задачи, описываемый соответствующей таблицею, удовлетворяет указанным ниже условиям.

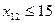
Поставщик (А_i)	Потребитель (B_j)				Запасы
Поставщик (А_i)	B₁	B₂	B₃	B₄	Запасы
А₁
А₂
А₃
Потребности					100/90

Общие суммарные затраты, которые связаны с перевозками, можно представить функцией

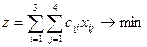в нашем случае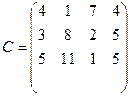

Построим функцию :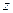

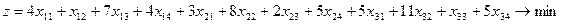
Переменные 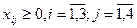отвечают условиям граничным по запасам и потребностям

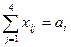
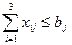
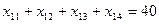
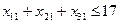
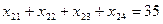
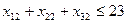
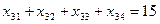
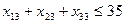
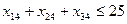
Дополнительное удовольствие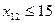

Наша задача представляет собой открытую модель транспортной задачи. Причем 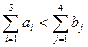. Для того, чтобы решить эту задачу, введем фиктивного поставщика, дополнительную строку, где 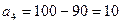, а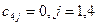

Тогда задачи примет вид

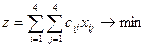
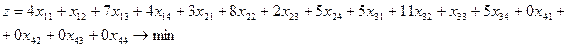
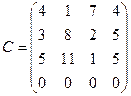
Используя метод меньшей цены, найдем опорный план.

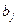
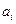
Метод наименьшей цены заключается в том, что выбирается из таблицы минимальный 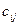за исключением 4 строки, в нашем случаи.

Шаг первый выбираем минимальный элемент. 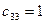, тогда 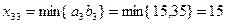. В результате запасы 3 поставщика использованы, поэтому исключаем из дальнейшего рассмотрения третью строку., 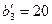.Получаем новую таблицу:





-	-	-

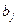
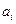
Шаг второй. Минимальный элемент 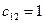, тогда 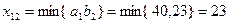, но с учётом условия задачи 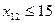. Поэтому допустим 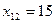. 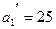, 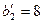.Получаем новую таблицу:





-	-	-

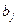
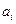
Продолжаем таким же образом, находим опорный план:



-		-
	-		-
-	-		-
		-	-

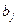
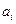
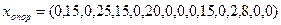
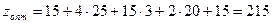ден. ед.

Применяя метод потенциалов, мы можем убедиться, что данный опорный план оптимален.

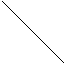
Для этого нужно вычислить потенциалы 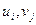, которые удовлетворяют условие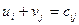

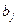
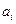
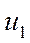
Для определения потенциалов, мы можем допустить, что один из коэффициентов равен нулю и найти другие.

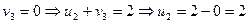
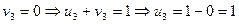
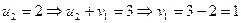
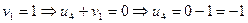
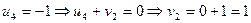
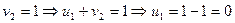
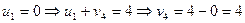
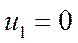
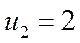
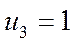
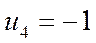
Проведем оценку потенциалов по формуле 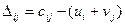и запишем их в левый угол каждой ячейки.



-			-
	-			-1	-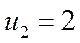
-	-					-
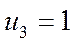
		-		-3		-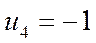

Поскольку есть 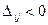, данное решение не является оптимальным.

Отыскиваем, какую циклическую замену можно произвести:

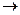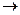(4,4) (1,4) (1,2) 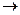(2,4). Такая замена приведет к увеличению значение 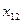, а это недопустимо, согласно наложенному условию. Поэтому данное решение является оптимальным.