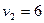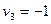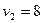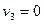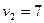Xоптимальный = (0, 15, 0, 25, 15, 0, 20, 0, 0, 0, 15, 0)
Z оптимальный=215 ден. ед.
Среди оптимальных планов транспортной задачи, описываемой соответствующей таблицей, найти план, удовлетворяющий указанным ниже условиям.
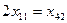 ,
, 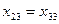
 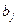 
| |||
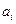
| |||
Решение:
Данная транспортная задача сводится к нахождению минимума целевой функции:
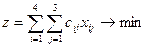 , где
, где 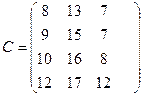
или
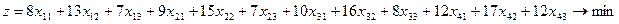
Поскольку 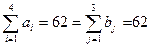 , то наша задача является сбалансированной или закрытой и переменные
, то наша задача является сбалансированной или закрытой и переменные 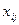 должны дополнительно удовлетворять условиям:
должны дополнительно удовлетворять условиям:
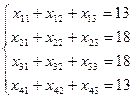 и
и 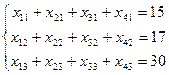 , где
, где 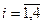 ,
, 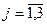
С помощью метода наименьшей цены найдем опорный план:
Шаг 1.
 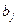 
| |||
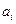
| |||
| 18 | |||
| 18 | |||
Минимальный среди всех 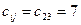 , тогда
, тогда 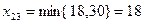 . А
. А 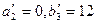 . Исключаем вторую строку из дальнейшего рассмотрения, так как второму поставщику ничего уже предложить.
. Исключаем вторую строку из дальнейшего рассмотрения, так как второму поставщику ничего уже предложить.
Шаг 2.
|
|
|
 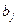 
| ||||
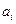
| ||||
| 0 | - | - | ||
| 18 | ||||
Минимальный среди всех 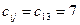 , тогда
, тогда 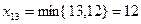 . А
. А 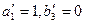
Исключаем третий столбец из дальнейшего рассмотрения, так как потребитель получил уже все требуемое количество товара.
Шаг 3.
 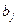 
| ||||
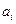
| ||||
| 0 | - | - | ||
| 18 | - | |||
| - | ||||
Минимальный среди всех 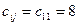 , тогда
, тогда 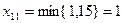 . А
. А 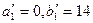
Исключаем первую строку из дальнейшего рассмотрения, так как поставщик исчерпал свои запасы.
Шаг 4.
 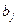 
| ||||||
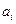
| ||||||
| - | ||||||
| 0 | - | - | ||||
| 18 | - | |||||
| - | ||||||
Минимальный среди всех 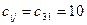 , тогда
, тогда 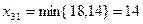 . А
. А 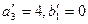
Исключаем первый столбец из дальнейшего рассмотрения, так как потребитель получил уже все требуемое количество товара.
Шаг 5.
 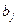 
| ||||||
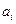
| ||||||
| - | ||||||
| 0 | - | - | ||||
| 4 | - | |||||
| - | - | |||||
Минимальный среди всех 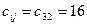 , тогда
, тогда 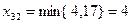 . А
. А 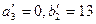
Исключаем третью строку из дальнейшего рассмотрения, так как поставщик уже поставил всю изготовленную продукцию.
Шаг 6.
 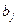 
| ||||||||
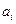
| ||||||||
| - | ||||||||
| 0 | - | - | ||||||
| 0 | - | |||||||
| - | - | |||||||
|
|
|
Получили опорный план
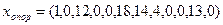
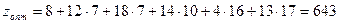 ден. ед.
ден. ед.
С помощью метода потенциалов проверим является ли данный опороный план оптимальным. Для этого вычисляем потенциалы и их оценку:
 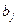 
| |||||||||||||
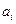
| |||||||||||||
  0 0
| -1 | - |
| ||||||||||
| 18 | - | - | |||||||||||
| 18 |  0 0
| -1 | - | ||||||||||
| - | - | ||||||||||||
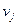
| 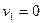
|
|
|
|
| ||||||||
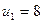
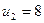
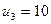
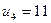
Найденное нами решение не является оптимальным, поскольку есть отрицательные оценки.
Для получения оптимального решения, нужно сделать циклическую замену.
Поскольку у нас наложено дополнительное условие 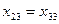 , то среди минимальных отрицательных оценок выберем
, то среди минимальных отрицательных оценок выберем 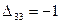 .
.
Цикл (3,3) 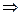 (1,3)
(1,3) 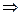 (1,1)
(1,1) 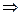 (3,1), таким образом клетка (3,3) включается в базис. Вершинам цикла присвоим знаки «+» и «–«начиная с (3,3). Затем выбираем из клеток со знаком -, с минимальным грузом. В нашем случае это клетка (1,3) и перераспределяем поставки, так что бы сохранились балансы для поставщика и потребителя. В минусовых вершинах будем отнимать минимальное значение, а в положительных прибавлять. Получим:
(3,1), таким образом клетка (3,3) включается в базис. Вершинам цикла присвоим знаки «+» и «–«начиная с (3,3). Затем выбираем из клеток со знаком -, с минимальным грузом. В нашем случае это клетка (1,3) и перераспределяем поставки, так что бы сохранились балансы для поставщика и потребителя. В минусовых вершинах будем отнимать минимальное значение, а в положительных прибавлять. Получим:
 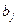 
| |||||||||||||
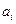
| |||||||||||||
| -1 | - | - | |||||||||||
| 18 | - | - | |||||||||||
| 18 | |||||||||||||
| - | - | ||||||||||||
| 
|
|
|
|
| ||||||||
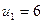
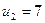
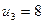
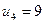
Найденное нами решение не является оптимальным, поскольку есть отрицательные оценки.
Для получения оптимального решения, нужно сделать циклическую замену.
Цикл (1,2) 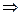 (1,1)
(1,1) 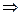 (3,1)
(3,1) 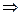 (3,2). Вершинам цикла присвоим знаки «+» и «–«начиная с (1,2). Затем выбираем из клеток со знаком -, с минимальным грузом. В нашем случае это клетка (1,3) и перераспределяем поставки, так что бы сохранились балансы для поставщика и потребителя. В минусовых вершинах будем отнимать минимальное значение, а в положительных прибавлять.
(3,2). Вершинам цикла присвоим знаки «+» и «–«начиная с (1,2). Затем выбираем из клеток со знаком -, с минимальным грузом. В нашем случае это клетка (1,3) и перераспределяем поставки, так что бы сохранились балансы для поставщика и потребителя. В минусовых вершинах будем отнимать минимальное значение, а в положительных прибавлять.
Получим:
 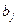 
| |||||||||||||
| |||||||||||||
| - | |||||||||||||
| 18 | - | - | |||||||||||
| 18 | - | ||||||||||||
| - | - | ||||||||||||
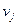
| 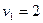
|
|
|
|
| ||||||||
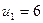
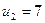
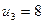
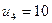
Данное решение является оптимальным. Но нам нужно решение, которое удовлетворяет условиям:
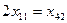 ,
, 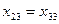
Для этого мы можем распределить груз, так что бы условия выполнялись:
 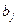 
| |||||||||||||
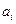
| |||||||||||||
|
|
| - | |||||||||||
| 18 |
| - |
| ||||||||||
| 18 |
| - |
| ||||||||||
| - | |||||||||||||
Ответ:
 2021-10-23
2021-10-23 46
46

 0
0