2014-02-13
519
1. Теорема Остроградского – Гаусса.
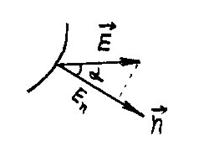
Потоком напряженности электрического поля сквозь малый участок поверхности, проведенный в поле, называется величина
,
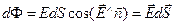где 
- вектор напряженности в точках поверхности 
, 
- единичный вектор, нормальный к площадке 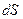, а вектор 
= 
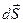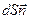. Так как 
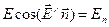- проекция напряженности поля 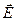на направление нормали, то 
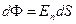(см. рис.).
Поток напряженности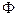 
сквозь любую поверхность 
равен
.
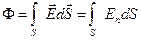При этом все векторы нормалей к малым поверхностям надо направлять по одну и ту же сторону относительно поверхности 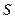.В случае замкнутой поверхности 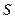всюду под 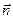понимается вектор внешних нормалей (см. рис).
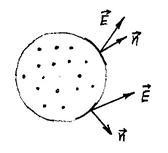
Найдем поток напряженности электростатического поля сквозь любую замкнутую поверхность, проведенную в этом поле. Допустим, что внутри замкнутой поверхности находятся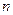 
точечных зарядов 
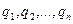. В силу принципа суперпозиции, напряженность поля 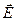, создаваемого всеми зарядами, равна геометрической сумме напряженностей 
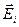, создаваемых каждым зарядом в отдельности
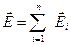(1)
Поэтому
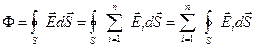. (2)
Подсчитаем
= 
= 
= 
= 
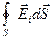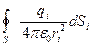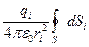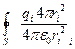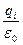. (3)
Подставим (3) в (2) и получим
.
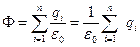Итак
= 
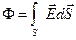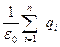. (4)
Выражение (4) – теорема Остроградского –Гаусса.
Поток вектора напряженности электрического поля через любую замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на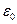 
.
Метод расчета полей, основанный на использовании принципа суперпозиции, применим к расчету поля любой системы зарядов. Это универсальный способ расчета полей, но он связан с математическими трудностями. Однако в случае полей симметричных систем зарядов удобно пользоваться теоремой Остроградского –Гаусса.
