Скорость движения жидкости в трубопроводе постоянного круглого сечения пропорциональна градиенту давления и квадрату радиуса трубы и обратно пропорциональна вязкости жидкости.
Рассмотрим движение жидкости по трубопроводу постоянного сечения (рис.13).
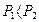
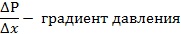
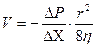
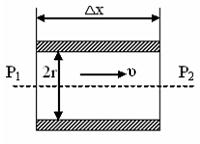
Рисунок 13.
Знак «- «в уравнении показывает, скорость жидкости направлена противоположно градиенту давления.
Уравнение неразрывности струи.
Рассмотрим движение жидкости по трубопроводу с непостоянным сечением (рис.14).
Так как жидкость не может выходить за боковые поверхности трубы и не сжимается, за единицу времени через сечение  и
и  пройдет одинаковый объем жидкости.
пройдет одинаковый объем жидкости.
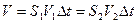
Если  =1, то
=1, то  , т.к. сечения
, т.к. сечения  и
и  выбраны абсолютно произвольно, то можно записать:
выбраны абсолютно произвольно, то можно записать:
 получили уравнение неразрывности струи произведение площади поперечного сечения трубы на скорость движения жидкости есть величина постоянная.
получили уравнение неразрывности струи произведение площади поперечного сечения трубы на скорость движения жидкости есть величина постоянная.
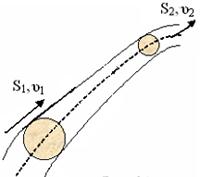
Рисунок 14.
Уравнение Бернулли.
Рассмотрим наклонную трубку тока с непостоянным сечением (рис.15).
Найдем изменение полной энергии, происходящие с этой системе за время  .
.
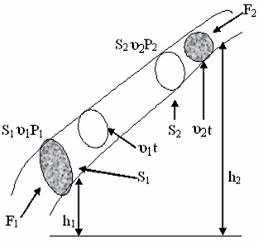
Рисунок 15.
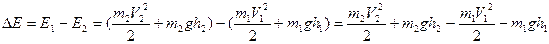
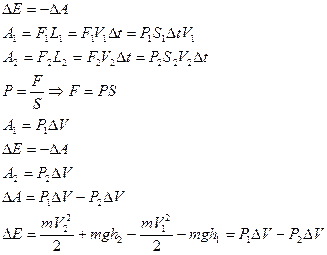
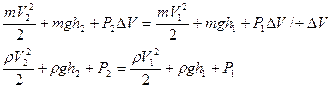
Т.к. сечения  и
и  выбраны произвольно, то можно записать:
выбраны произвольно, то можно записать:
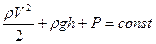
Уравнение Бернулли. В установившемся потоке идеальной жидкости полное давление складывающиеся из суммы – динамическое, гидравлического и статистического – есть величина постоянная.
Рассмотрим размерность, чтобы увидеть физический смысл выражения
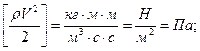
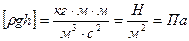
рgh - гидравлическое давление
 2014-02-13
2014-02-13 1073
1073

 -
-  -
- 






