2014-02-13
2602
Тогда
,
.
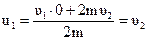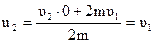Если до столкновения второй шар покоился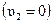 
, то после столкновения первый шар остановился 
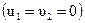, а второй будет двигаться со скоростью 
.
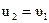2) Масса второго шара значительно больше массы первого (т2 >> т1). Разделим числитель и знаменатель выражений (4.14) и (4.15) на m2:
;
.
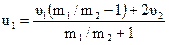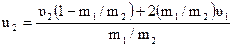Отношением 
m1/m2 пренебрегаем. Тогда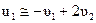 
, 
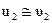, т.е. скорость большого шара практически не меняется.
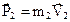
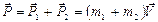
Если массивный шар покоился 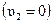, то он покоится и после удара 
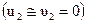, а малый шар будет иметь скорость 
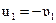. Такой тип столкновения рассматривается при расчете давления, оказываемого молекулами газа на стенки сосуда.
Пусть абсолютно не упруго сталкиваются два тела с массами m1 и m2, движущихся со скоростям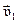и 
и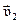 
. Считаем, что тела образуют замкнутую систему. По закону сохранения импульса
.
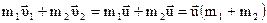Отсюда скорость после столкновения равна
.
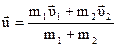Из этой формулы видно, что после столкновения тела двигаются вдоль диагонали параллелограмма, построенного на векторах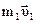 
и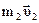 
.
Закон сохранения суммарной энергии в случае абсолютно неупругого удара запишется в виде
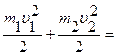
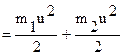+ Адеформ.
