Закон сохранения момента импульса. Вращательное движение отдельного тела определятся уравнениями

Вращательное движение отдельного тела определятся уравнениями

, ,

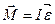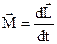где 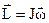- момент импульса тела в плоскости относительно некоторой точки О через которую проходит ось вращения Z(рис 4.2).

Модуль момента импульса материальной точки.

.

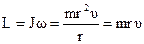Учитывая, что 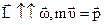, а 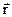- есть радиус вектор, соединяющий точку О с центром инерции тела, то можно записать

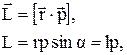
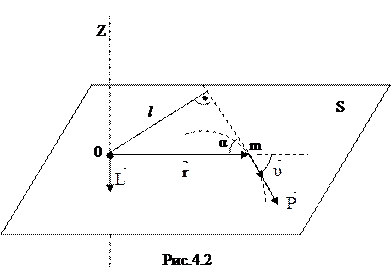
где 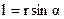- плечо вектора 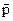относительно точки О.

Вектор 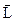направлен вдоль оси Z и совпадает с поступательным движением правого винта (буравчика), если он вращается от вектора 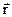к 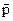по кратчайшему пути.

Закон сохранения момента импульса отдельного тела определяется из соотношения

.

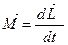Если .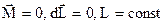

Если результирующий момент M всех внешних сил, действующих на тело, равен нулю, то момент импульса тела остаётся постоянным.

Рассмотрим систему из двух материальных точек вращающихсяв плоскости S вокруг оси проходящей через точку О взаимодействующих между собой и с внешними телами (рис 4.3)

.

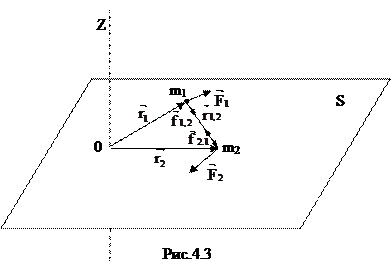
В произвольный момент времени t моменты импульсов этих тел , .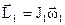

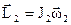Изменение момента импульса каждого из тел обусловлено действием как внутренних, так и внешних моментов сил .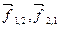

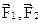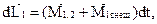
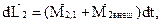
где , ,.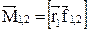

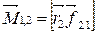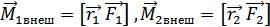Изменение момента импульса системы тел

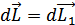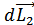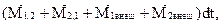+= (4.5)