Закон сохранения четности

Назовем преобразованием инверсии (или четности) оператор, который следующим образом действует на произвольную функцию:

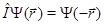(10)

Очевидно, оператор четности имеет два собственных значения - это +1 и –1. Действительно, подействуем на уравнение на собственные значения и собственные функции оператора инверсии

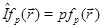(11)

оператором инверсии (здесь 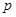- собственное значение оператора инверсии, 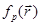- отвечающая ему собственная функция)

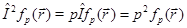(12)

В результате с учетом того, что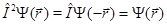, имеем

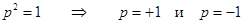(13)

Очевидно, собственные функции, отвечающие собственному значению 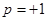- любые четные функции, отвечающие собственному значению 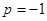- любые нечетные. Среднее значение оператора четности в любом состоянии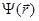

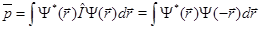(14)

показывает, насколько волновая функция этого состояния близка к четной или нечетной функции. Действительно, если волновая функция четная из (14) и условия нормировки получаем, что 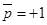. Если волновая функция нечетная - .

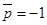Рассмотрим частицу, движущуюся в некотором потенциале 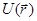. Если потенциальная энергия не меняется при преобразовании инверсии, то оператор инверсии коммутирует с гамильтонианом 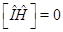. В этом случае четность является интегралом движения. В частности, если потенциальная энергия четная функция, а волновая функция частицы в начальный момент времени имеет определенную четность (является либо четной, либо нечетной функцией координат), то она останется таковой и любой последующий момент времени.

В заключение этой лекции подчеркнем, что для сохранения физической величины в квантовой механики нужна независимость от времени ее среднего значения, результаты же отдельных измерений могут быть различными. Для иллюстрации этого утверждения рассмотрим состояние

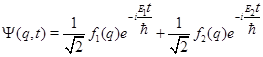(15)

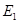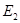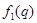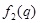где и - собственные значения не зависящего от времени оператора Гамильтона, и - отвечающие им нормированные собственные функции. Согласно основным принципам квантовой механики энергия в состоянии (15) определенного значения не имеет, и при измерениях могут быть получены два значения 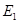и 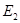с одинаковыми вероятностями. Это значит, что мы не можем утверждать, что результаты любых измерений энергии будут одинаковыми. Можно утверждать, что если выполнить много измерений над ансамблем тождественных квантовых систем с волновой функцией (12) в некоторый момент времени и усреднить эти результаты, то это среднее значение не будет зависеть от времени. Для рассматривае6мого состояния согласно основным принципам квантовой механики имеем

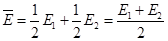(16)