Зависимость средних от времени. Интегралы движения. Законы сохранения и симметрии. Сохранение четности

Эволюция квантовой системы во времени определяется временным уравнением Шредингера

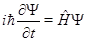(1)

Поскольку это уравнение является уравнением первого порядка по времени, для однозначного нахождения решения необходимо задать волновую функцию системы в начальный момент времени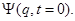

Как было показано на предыдущей лекции, в случае, когда гамильтониан не зависит явно от времени, общее решение уравнения (1) может быть найдено в квадратурах

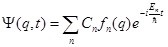(2)

где 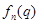- собственные функции оператора Гамильтона, 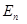- соответствующие собственные значения, 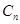- произвольные постоянные. Таким образом, для нахождения всех возможных решений временного уравнения Шредингера необходимо знать все решения уравнения на собственные значения и собственные функции оператора Гамильтона

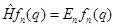(3)

По этой причине уравнение (3) играет для квантовой механики столь же фундаментальное значение, что и уравнение Шредингера, и потому (?) также называется уравнением Шредингера. Чтобы не путать эти два (совершенно разных) уравнения первое принято называть временным уравнением Шредингера, второе – стационарным уравнением Шредингера.

Чтобы исследовать зависимость средних от времени найдем оператор производной физической величины по времени.

Пусть есть некоторая физическая величина 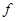и ей соответсвует оператор 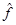. Найдем, какой оператор будет соответствовать величине 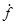, то есть найдем вид оператора .

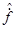По определению в любом состоянии должно быть выполнено следующее равенство:

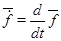(4)

Далее воспользуемся квантовомеханической формулой для средних и временным уравнением Шредингера. В результате получим следующее.

В правой части формулы (4):

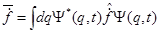(5)

где 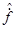- искомый оператор производной величины 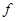по времени.

В левой части (4):

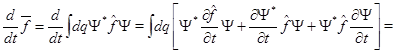
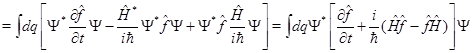(6)

Сравнивая (5), (6) и учитывая, что равенство (4) должно быть справедливо в состоянии с произвольной волновой функцией 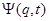, заключаем:

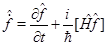(7)

Из формулы (7) следует, что если оператор некоторой физической величины не зависит явно от времени и коммутирует с оператором Гамильтона, то среднее значение данной физической величины не зависит от времени в любом состоянии, поскольку производная от среднего значения равна нулю.

Здесь можно провести определенную аналогию с классической механикой. В классической механике для производной функции 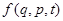динамических переменных – координат и импульсов – по времени справедливо соотношение:

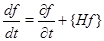
где 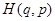- функция Гамильтона, 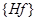- скобка Пуассона функции Гамильтона 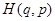и функции 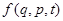. Из этой формулы следует, что при переходе от квантовой механики к классической коммутатор операторов переходит в их классическую скобку Пуассона

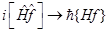
В квантовой механике интегралами движения называют такие физические величины, средние значения которых в любых состояниях не зависят от времени. Из формулы (4) следует, что для того чтобы физическая величина была интегралом движения оператор этой величины не должен не зависеть явно от времени и должен коммутировать с оператором Гамильтона.

Поскольку факт коммутации ряда операторов физических величин с оператором Гамильтона следует из свойств симметрии пространства-времени, поэтому в квантовой механике (так же, как и в классической механике) существование ряда интегралов движения связано с симметриями пространства-времени.