Алгоритм Флойда. Обозначим lij длину дуги (xi, xj), если таковой не существует примем lij = ¥, кроме того, положим lii = 0

Обозначим l_ij длину дуги (x_i, x_j), если таковой не существует примем l_ij = ¥, кроме того, положим l_ii = 0. Обозначим 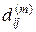длину кратчайшего из путей из x_i в x_j с промежуточными вершинами из множества { x ₁, …, x_m }. Тогда можно получить следующие уравнения

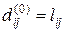, (2)

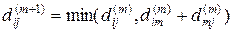. (3)

Уравнение (2) очевидно. Обоснуем уравнение (3). Рассмотрим кратчай­ший путь из x_i в x_j с промежуточными вершинами из множества { x ₁, …, x_m, x_{m +1}}. Если этот путь не содержит x_{m +1}, то 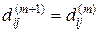. Если же он содержит x_{m +1}, то деля путь на отрезки от x_i до x_{m +1} и от x_{m +1} до x_j, получаем равенство .

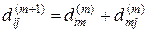Уравнения (2) и (3) позволяют легко вычислить матрицу расстояний [ d_ij ] между всеми парами вершин графа G (X, E). На первом этапе согласно (2) составляем n ´ n матрицу 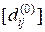равную матрице [ l_ij ] весов ребер (n – число вершин G (X, E)). n раз производим вычисление по итерационной формуле (3), после чего имеем 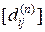– матрицу расстояний.

Отметим, что алгоритм Флойда непосредственно не указывает сам кратчайший путь между вершинами, а только его длину. Алгоритм Флойда можно модифицировать таким образом, чтобы можно было находить и сами пути. Для этого получим вспомогательную матрицу [ R_ij ], которая будет содержать наибольший номер вершины некоторого кратчайшего пути из x _i в x _j (R_ij =0, если этот путь не содержит промежуточных вершин).

Эта матрица вычисляется параллельно с 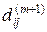по следующим правилам

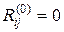
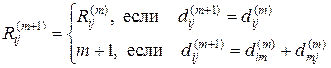
Последнее выражение следует из обоснования (3).

Теперь кратчайший путь выписывается из следующего рекурсивного алгоритма:

Кратчайший путь из x_i в x_j:

1°. Если R_ij = 0 то выполнить 2°,

иначе выполнить 3°.

2°. Если i = j то выписать x_i и закончить,

иначе выписать x_i и x_j закончить.

3°. Выписать кратчайший путь между x_i и .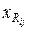

4°. Выписать кратчайший путь между 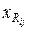и x_j.

Пункты 3° и 4° предполагают рекурсивное обращение к рассмотренному алгоритму.

С задачей определения кратчайших путей в графе тесно связана задача транзитивного замыкания бинарного отношения.

Напомним, что бинарным отношением на множестве Х называется произвольное подмножество E Ì X ´ X.

Транзитивным называется отношение, удовлетворяющее следующему условию: если (x, y) Î E и (y, z) Î E, то (x, z) Î E для всех x, y, z Î X. Отметим, что бинарное отношение можно однозначно представить орграфом G (X, E). Теперь для произвольного отношения Е определим новое отношение Е * следующим образом

E * = {(x, y) | если в G (X, E) существует путь ненулевой длины из x в y }.

Легко проверить, что Е * - транзитивное отношение. Кроме того, Е * является наименьшим транзитивным отношением на Х в том смысле, что для произвольного транзитивного отношения F É E выполняется E * É F. Отно­ше­ние Е * называется транзитивным замыканием отношения Е.

Если отношение Е представить в виде графа G (X, E) в котором каждая дуга имеет вес 1, то транзитивное замыкание Е * можно вычислить с помощью алгоритма Флойда. При этом надо учесть, что

(x_i, x_j) Î E * если .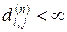

Для большего удобства алгоритм Флойда в этом случае можно моди­фи­ци­ровать следующим образом.

Положим

.

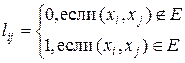Вместо (3) запишем

,

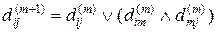где Ú – дизъюнкция (логическое сложение),

Ù – конъюнкция (логическое умножение).

После завершения работы алгоритма будем иметь

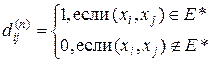
Модифицированный таким образом алгоритм называется алгоритмом Уоршелла.

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ

[1] Система переключательных функций называется независимой, если ни одна из входящих в нее функций не выражается через другие функции этой же системы с помощью операций суперпозиции или подстановки аргументов.