2.1. Корень алгебраического многочлена и его кратность
Пусть n – заданное натуральное число, а 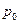 ,
, 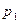 , ¼,
, ¼, 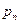 – заданные комплексные числа. Выражение
– заданные комплексные числа. Выражение
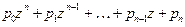 , где z
, где z 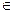 С назовем алгебраическим многочленом степени не выше n и обозначим через
С назовем алгебраическим многочленом степени не выше n и обозначим через  :
: 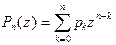 . Числа
. Числа 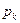 , k = 0, 1, ¼, n, называют коэффициентами мно- гочлена
, k = 0, 1, ¼, n, называют коэффициентами мно- гочлена  ,
, 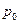 называют старшим коэффициентом этого многочлена.
называют старшим коэффициентом этого многочлена.
Если 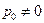 ,
,  назовем многочленом степени n. Если
назовем многочленом степени n. Если 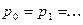
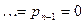 , то
, то  назовем многочленом степени 0; в этом случае, очевидно, " z Î C
назовем многочленом степени 0; в этом случае, очевидно, " z Î C 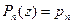 .
.
Пусть 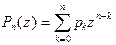 ,
,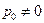 ,- многочлен степени n, n ³ 1, и пусть a – некото- рое комплексное число. Поделим
,- многочлен степени n, n ³ 1, и пусть a – некото- рое комплексное число. Поделим  на двучлен z – a. Результат запишем в виде равенства
на двучлен z – a. Результат запишем в виде равенства 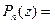
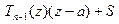 , справедливого при всех комплексных z. Здесь
, справедливого при всех комплексных z. Здесь 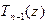 - многочлен степени n- 1 (частное), а S – число (остататок). Найти
- многочлен степени n- 1 (частное), а S – число (остататок). Найти 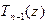 и S можно с помощью процедуры деления “уголком”, известной из школьного курса ал- гебры. Если S
и S можно с помощью процедуры деления “уголком”, известной из школьного курса ал- гебры. Если S 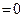 , говорят, что
, говорят, что  делится на z – a без остатка.
делится на z – a без остатка.
Замечание 1. При делении многочлена  на z – a старший коэффициент частного
на z – a старший коэффициент частного 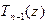 равен старшему коэффициенту
равен старшему коэффициенту  , т.е.,
, т.е., 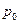 .
.
Пусть  - некоторый многочлен, a - некоторое комплексное число. Если
- некоторый многочлен, a - некоторое комплексное число. Если 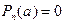 , то число a называют корнем алгебраического многочлена
, то число a называют корнем алгебраического многочлена 
Фундаментальную роль играет следующая теорема, которая принадлежит К. Гауссу и которую обычно называют основной теоремой алгебры.
Теорема 1 ( Гаусс ). Всякий алгебраический многочлен степени n, n ³ 1, имеет хотя бы один корень.
Доказательство этой теоремы средствами теории функций комплексного пере- менного будет приведено позже.
Теорема 2 ( Безу ). Пусть 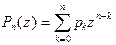 ,
,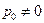 , – некоторый многочлен степени n, n ³ 1, и пусть a Î C – некоторое число. Для того, чтобы a являлось кор- нем
, – некоторый многочлен степени n, n ³ 1, и пусть a Î C – некоторое число. Для того, чтобы a являлось кор- нем  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы  без остатка делился на разность z – a
без остатка делился на разность z – a
 Необходимость. Поделив
Необходимость. Поделив  на
на 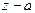 , получим:
, получим:
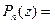
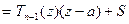 , где S Î C. Подставим в это равенство z = a:
, где S Î C. Подставим в это равенство z = a: 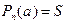 ; так как a - корень
; так как a - корень  , то
, то 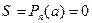 .
.
Достаточность. Пусть 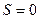 ; тогда
; тогда 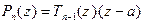 . Подставив z = a, получим:
. Подставив z = a, получим: 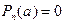 , т.е. a – корень
, т.е. a – корень  .
. 
Следствие. Пусть 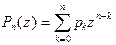 ,
,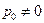 , – многочлен степени n, n ³ 1, и пусть a, a Î C, – корень этого многочлена. Существуют натуральное число k, 1 £ k £ n, и многочлен
, – многочлен степени n, n ³ 1, и пусть a, a Î C, – корень этого многочлена. Существуют натуральное число k, 1 £ k £ n, и многочлен 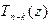 степени n – k такие, что
степени n – k такие, что 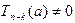 и " z Î C
и " z Î C
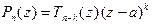 . (14)
. (14)
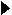 Поделив
Поделив  на z – a, получим в силу теоремы Безу:
на z – a, получим в силу теоремы Безу:
" z Î C 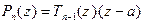 , (15) где
, (15) где 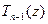 - многочлен степени n -1, старший коэффициент которого равен
- многочлен степени n -1, старший коэффициент которого равен 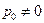 (см. замечание 1).
(см. замечание 1).
Возможны два случая: 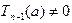 и
и 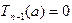 . В первом случае утверждение теоремы справедливо, так как (15) есть (14) при k = 1. Во втором случае a является кор- нем
. В первом случае утверждение теоремы справедливо, так как (15) есть (14) при k = 1. Во втором случае a является кор- нем 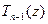 и потому
и потому 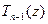 делится на z – a без остатка:
делится на z – a без остатка: 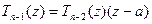 , где
, где 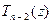 - многочлен степени n - 2. Подставив в (15), получим:
- многочлен степени n - 2. Подставив в (15), получим:
" z Î C 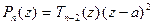 . (16)
. (16)
Возможны два случая: 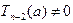 и
и 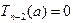 . В первом случае утверждение теоремы справедливо. так как (16) есть (14) при k = 2. Во втором случае поделим
. В первом случае утверждение теоремы справедливо. так как (16) есть (14) при k = 2. Во втором случае поделим 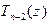 на z – a:
на z – a: 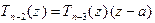 . Отсюда:
. Отсюда:
" z Î C 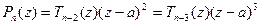 , и снова рассматриваем два случая:
, и снова рассматриваем два случая: 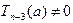 и
и 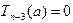 . Описываемый процесс приводит к построению последовательности многочленов
. Описываемый процесс приводит к построению последовательности многочленов 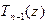 ,
, 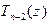 , ¼,
, ¼, 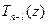 где каждый последующий многочлен получен делением предыдущего на разность z – a, причем (см. замечание 1) старший коэффициент каждого из них равен
где каждый последующий многочлен получен делением предыдущего на разность z – a, причем (см. замечание 1) старший коэффициент каждого из них равен 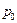 . Так как степень частного на единицу ниже степени делимого, то эта последовательность состо- ит не более чем из n многочленов, а последний многочлен
. Так как степень частного на единицу ниже степени делимого, то эта последовательность состо- ит не более чем из n многочленов, а последний многочлен 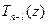 уже не делится на z – a без остатка, ибо
уже не делится на z – a без остатка, ибо 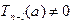 . Завершив построение указанной последовательности, получим:
. Завершив построение указанной последовательности, получим:
" z Î C 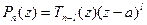 , где
, где 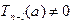 , т.е. получим равенство (14) при k = l, l
, т.е. получим равенство (14) при k = l, l 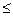 n.
n. 
Замечание 2. При k = n представление (14) выглядит так:
" z Î C 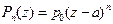 . (17)
. (17)
Замечание 3. Число k в представлении (14) определяется единственным обра- зом. Действительно, допустим, что имеются два таких представления: " z Î C
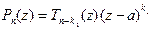 и
и 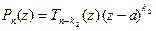 , где
, где 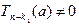 ,
, 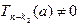 . Допустим, что
. Допустим, что 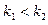 . Имеем:
. Имеем: 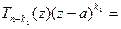 =
= 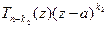 . Так как
. Так как 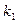 и
и 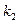 – натуральные числа и
– натуральные числа и 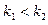 , то
, то 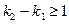 . Подставив z = a, получим:
. Подставив z = a, получим: 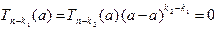 , что противоречит усло- вию
, что противоречит усло- вию 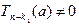 . Возможность
. Возможность 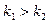 опровергается аналогично. Значит,
опровергается аналогично. Значит, 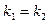 .
.
Число k в представлении (14) называют кратностью корня a.
Замечание 4. Число a является корнем кратности k многочлена  тогда и только тогда, когда этот многочлен без остатка делится на
тогда и только тогда, когда этот многочлен без остатка делится на 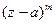 при m = 1, 2, ¼, k и не делится на
при m = 1, 2, ¼, k и не делится на 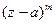 при m > k.
при m > k.
Это утверждение легко следует из (14).
Если кратность корня a многочлена  равна единице, его называют прос- тым корнем этого многочлена.
равна единице, его называют прос- тым корнем этого многочлена.
2.2 Разложение многочлена на линейные множители
Теорема 3. (О разложении многочлена на линейные множители)
Пусть 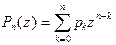 – алгебраический многочлен степени n, n ³ 1. Тогда:
– алгебраический многочлен степени n, n ³ 1. Тогда:
1)  имеет не более n попарно различных корней;
имеет не более n попарно различных корней;
2) если 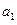 ,
, 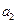 , ¼,
, ¼, 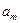 , m £ n, – все попарно различные корни
, m £ n, – все попарно различные корни  , а
, а 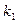 ,
, 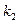 ,¼,
,¼, 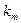 – кратности этих корней (
– кратности этих корней (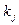 есть кратность
есть кратность 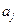 ), то
), то
а) сумма всех кратностей равна степени многочлена: 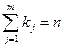 ;
;
б) справедливо представление:
" z Î C 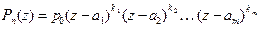 . (18)
. (18)
 По теореме Гаусса существует хотя бы один корень
По теореме Гаусса существует хотя бы один корень  . Пусть
. Пусть 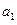 - корень
- корень  , а
, а 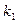 - его кратность. Тогда (см. (14)):
- его кратность. Тогда (см. (14)):
" z Î C 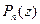
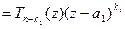 , причем
, причем 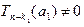 . Возможны два случая:
. Возможны два случая: 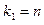 и
и 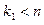 . В первом случае справедливо представление (см. (17)): " z Î C
. В первом случае справедливо представление (см. (17)): " z Î C 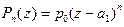 , т.е., справедливо (18) при m =1. Во втором случае степень
, т.е., справедливо (18) при m =1. Во втором случае степень 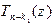 не меньше единицы, и по теореме Гаусса существует корень этого многочлена.
не меньше единицы, и по теореме Гаусса существует корень этого многочлена.
Пусть 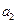 - корень
- корень 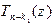 , а
, а 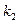 - кратность этого корня. Очевидно,
- кратность этого корня. Очевидно, 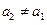 . Имеем (см. (14): " z Î C
. Имеем (см. (14): " z Î C 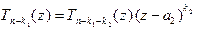 , где
, где 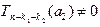 . Отсюда:
. Отсюда:
" z Î C 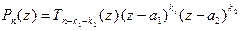 .
.
Возможны два случая: 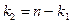 , т.е.
, т.е. 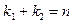 , и
, и 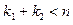 . В первом случае
. В первом случае 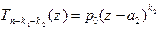 , поэтому
, поэтому 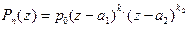 . Следовательно,
. Следовательно,  имеет два корня
имеет два корня 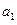 и
и 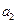 , и (18) справедливо при m =2. Во втором случае степень многочлена
, и (18) справедливо при m =2. Во втором случае степень многочлена 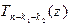 не меньше единицы, значит, существует корень
не меньше единицы, значит, существует корень 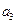 этого многочлена. Если
этого многочлена. Если 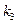 - кратность
- кратность 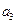 , то
, то 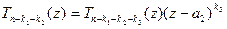 и
и
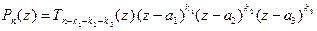 ,
,
Снова возможны случаи 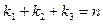 и
и 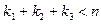 . В первом из них " z Î C
. В первом из них " z Î C 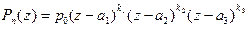 - представление (18) при m = 3, во втором – существует корень
- представление (18) при m = 3, во втором – существует корень 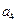 многочлена
многочлена 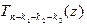 , и рассуждения можно продолжить. Конечным их результатом и будет представление (18), сумма кратностей в котором равна n. Так как кратность всякого корня – натуральное число, а сумма кратностей равна n, то количество попарно различных корней многочлена не может превышать n.
, и рассуждения можно продолжить. Конечным их результатом и будет представление (18), сумма кратностей в котором равна n. Так как кратность всякого корня – натуральное число, а сумма кратностей равна n, то количество попарно различных корней многочлена не может превышать n. 
Представление (18) называют разложением многочлена  на линейные множители.
на линейные множители.
Замечание 5. Если 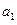 ,
, 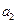 , ¼,
, ¼, 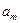 - все попарно различные корни многочлена
- все попарно различные корни многочлена  , то сумма их кратностей равна степени многочлена. Этот результат часто форму- лируют так: всякий алгебраический многочлен степени n, n ³ 1, имеет ровно n кор- ней с учетом их кратностей (т.е. если каждый корень учитывать столько раз, какова его кратность).
, то сумма их кратностей равна степени многочлена. Этот результат часто форму- лируют так: всякий алгебраический многочлен степени n, n ³ 1, имеет ровно n кор- ней с учетом их кратностей (т.е. если каждый корень учитывать столько раз, какова его кратность).
Пример. Пусть 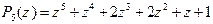 . Прямой подстановкой
. Прямой подстановкой 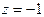 нетрудно убедиться, что это число является корнем
нетрудно убедиться, что это число является корнем 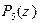 . Значит,
. Значит, 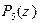 делится на разность
делится на разность 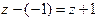 . Произведя деление, получим:
. Произведя деление, получим:
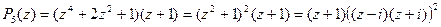 .
.
Таким образом, 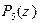 имеет три различных корня: простой корень –1 и корни ± i, кратность каждого из которых равна 2. Представление (18) для него выглядит так:
имеет три различных корня: простой корень –1 и корни ± i, кратность каждого из которых равна 2. Представление (18) для него выглядит так:
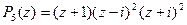
Следствие 1. Пусть 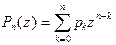 есть многочлен степени не выше n, и пусть каждое из n + 1 попарно различных чисел
есть многочлен степени не выше n, и пусть каждое из n + 1 попарно различных чисел 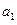 ,
, 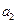 , ¼,
, ¼, 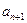 является корнем
является корнем  :
: 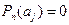 , j = 1, 2, ¼, n + 1. Тогда все коэффициенты
, j = 1, 2, ¼, n + 1. Тогда все коэффициенты  равны нулю, т.е.
равны нулю, т.е. 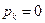 , k = 0, 1, ¼, n, и, следовательно,
, k = 0, 1, ¼, n, и, следовательно,  тождественно на C равен нулю.
тождественно на C равен нулю.
 является алгебраическим многочленом, степень которого не превышает n. Значит, количество попарно различных корней
является алгебраическим многочленом, степень которого не превышает n. Значит, количество попарно различных корней 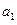 ,
, 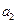 , ¼,
, ¼, 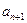 этого многочлена (их n + 1) больше его степени. Согласно теореме 3, если степень многочлена является на- туральным числом n, то количество его попарно различных корней не может превы- сить n. Значит, степень многочлена
этого многочлена (их n + 1) больше его степени. Согласно теореме 3, если степень многочлена является на- туральным числом n, то количество его попарно различных корней не может превы- сить n. Значит, степень многочлена  не может быть натуральным числом, т. е.,
не может быть натуральным числом, т. е.,  является многочленом степени 0. В таком случае
является многочленом степени 0. В таком случае 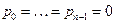 , и
, и 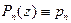 . Но
. Но 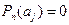 , поэтому и
, поэтому и 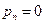 . Таким образом, все коэффициенты
. Таким образом, все коэффициенты  равны нулю.
равны нулю. 
Следствие 2. Пусть многочлены 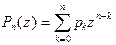 и
и 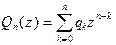 при- нимают совпадающие значения в n + 1 попарно различных точках
при- нимают совпадающие значения в n + 1 попарно различных точках 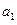 ,
, 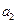 , ¼ …,
, ¼ …,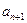 :
: 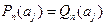 , j = 1, 2, ¼, n + 1. Тогда наборы коэффициентов
, j = 1, 2, ¼, n + 1. Тогда наборы коэффициентов  и
и 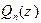 одинаковы:
одинаковы: 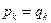 при всех k = 0, 1, ¼, n.
при всех k = 0, 1, ¼, n.
 Обозначим:
Обозначим: 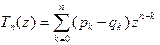 . При каждом j, j = 1, 2, ¼, n + 1, имеем
. При каждом j, j = 1, 2, ¼, n + 1, имеем 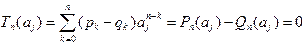 , т.е. многочлен
, т.е. многочлен 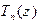 имеет n + 1 попарно различных корней. По следствию 1 все его коэффициенты равны нулю
имеет n + 1 попарно различных корней. По следствию 1 все его коэффициенты равны нулю 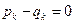 , k = 0, 1, ¼, n. Отсюда:
, k = 0, 1, ¼, n. Отсюда: 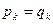 , k = 0, 1, ¼, n.
, k = 0, 1, ¼, n. 
Пусть  и
и 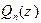 - два многочлена. Будем говорить, что они равны и запи- сывать при этом
- два многочлена. Будем говорить, что они равны и запи- сывать при этом 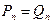 , если их значения совпадают при всех комплексных z:
, если их значения совпадают при всех комплексных z:
" z Î C 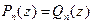 .
.
Следствие 3. Пусть 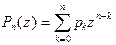 ,
, 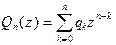 . Для того, чтобы эти два многочлена были равны, необходимо и достаточно, чтобы совпадали наборы их коэффициентов.
. Для того, чтобы эти два многочлена были равны, необходимо и достаточно, чтобы совпадали наборы их коэффициентов.
 Необходимость. Пусть
Необходимость. Пусть 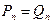 , т.е. " z Î C
, т.е. " z Î C 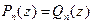 . Выберем какие – нибудь попарно различные числа
. Выберем какие – нибудь попарно различные числа 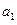 ,
, 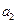 , ¼,
, ¼, 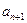 . Из " z Î C
. Из " z Î C 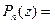
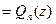 следует:
следует: 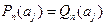 , j = 1, 2, ¼, n + 1. По следствию 2
, j = 1, 2, ¼, n + 1. По следствию 2 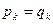 , k = 0, 1, ¼, n.
, k = 0, 1, ¼, n.
Достаточность очевидна: если 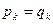 , k = 0, 1, ¼, n, то " z Î C
, k = 0, 1, ¼, n, то " z Î C
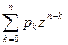
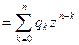 .
. 
Замечание 6. Пусть значения многочленов  и
и 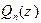 совпадают во всех точках вещественной оси: " х Î R
совпадают во всех точках вещественной оси: " х Î R 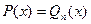 .Тогда их значения совпадают на всей комплексной плоскости: " z Î C
.Тогда их значения совпадают на всей комплексной плоскости: " z Î C 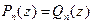 .
.
 Выберем попарно различные точки
Выберем попарно различные точки 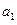 ,
, 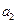 , ¼,
, ¼, 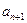 на вещественной оси. Имеем:
на вещественной оси. Имеем: 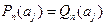 , j = 1, 2, ¼, n + 1. По следствию 2 наборы коэффициентов этих многочленов совпадают, а тогда " z Î C
, j = 1, 2, ¼, n + 1. По следствию 2 наборы коэффициентов этих многочленов совпадают, а тогда " z Î C 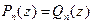 .
. 
2.3. Вещественные многочлены
Алгебраический многочлен 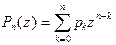 называют вещественным многочленом, если все его коэффициенты – вещественные числа. Значения, принима- емые вещественным многочленом в точках вещественной оси, являются веществен- ными числами.
называют вещественным многочленом, если все его коэффициенты – вещественные числа. Значения, принима- емые вещественным многочленом в точках вещественной оси, являются веществен- ными числами.
Теорема 4. (О корнях вещественного многочлена) Пусть  – вещественный алгебраический многочлен степени n, n ³ 1, и пусть a, a Î C, – корень этого много- члена кратности k. Тогда сопряжённое число
– вещественный алгебраический многочлен степени n, n ³ 1, и пусть a, a Î C, – корень этого много- члена кратности k. Тогда сопряжённое число 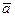 также является корнем
также является корнем  , причем той же кратности k.
, причем той же кратности k.
 Так как a - корень кратности k, то справедливо представление (14):
Так как a - корень кратности k, то справедливо представление (14):
" z Î C 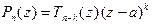 , где
, где 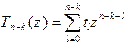 , причем
, причем 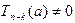 . Отсюда (см. п. 1.7): " z Î C
. Отсюда (см. п. 1.7): " z Î C
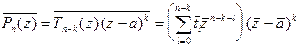 . В частности, эти равенства справедливы при вещественных z. Если z = x Î R, то
. В частности, эти равенства справедливы при вещественных z. Если z = x Î R, то 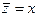 ; кроме того,
; кроме того, 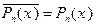 , так как при всяком x Î R
, так как при всяком x Î R 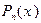 есть вещественное число. Отсюда: " x Î R
есть вещественное число. Отсюда: " x Î R
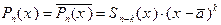 , где
, где 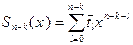 . Обозначим:
. Обозначим: 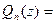
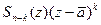 . Значения многочленов
. Значения многочленов  и
и 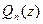 совпадают во всех точках вещественной оси; следовательно (см. заме- чание 6, п. 2.2), их значения совпадают во всех точках комплексной плоскости:
совпадают во всех точках вещественной оси; следовательно (см. заме- чание 6, п. 2.2), их значения совпадают во всех точках комплексной плоскости:
" z Î C 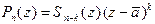 .
.
Заметим, что 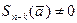 . Действительно,
. Действительно, 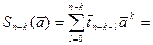
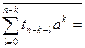
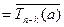 . Но
. Но 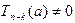 , значит, и
, значит, и 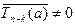 .
.
Таким образом, " z Î C 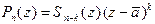 , причем
, причем 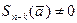 . Сле- довательно (см. (14)), число
. Сле- довательно (см. (14)), число 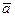 является корнем
является корнем  кратности k.
кратности k. 
Пусть 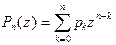 - вещественный многочлен степени n, n ³ 1, и пусть
- вещественный многочлен степени n, n ³ 1, и пусть 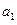 ,
, 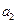 , ¼,
, ¼, 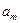 , m £ n, – все попарно различные его корни, а
, m £ n, – все попарно различные его корни, а 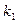 ,
, 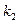 , ¼,
, ¼, 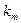 – кратности этих корней. Тогда справедливо представление (18). Допустим, что
– кратности этих корней. Тогда справедливо представление (18). Допустим, что 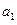 – мнимое число:
– мнимое число: 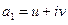 , где
, где 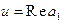 ,
, 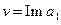 , причем n ¹ 0. По теореме 4 число
, причем n ¹ 0. По теореме 4 число 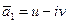 также является корнем
также является корнем  кратности
кратности 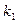 . Значит, в (18) среди множителей
. Значит, в (18) среди множителей 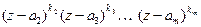 присутствует множитель
присутствует множитель 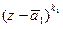 . Заметим:
. Заметим: 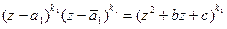 , где
, где 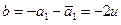 ,
, 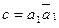 =
= 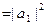 . Таким образом, объединив множители, отвечающие паре мнимых сопряженных корней а и
. Таким образом, объединив множители, отвечающие паре мнимых сопряженных корней а и 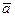 , получаем квадратный трехчлен с вещественными коэффициентами, возведенный в степень, равную кратности каждого из этих сопряженных корней.
, получаем квадратный трехчлен с вещественными коэффициентами, возведенный в степень, равную кратности каждого из этих сопряженных корней.
Пусть, как и выше,  , n ³ 1, – вещественный многочлен, а
, n ³ 1, – вещественный многочлен, а 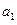 ,
, 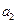 , ¼,
, ¼, 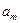 – все его попарно различные корни. Среди них могут быть и вещественные числа, и мнимые. Пусть
– все его попарно различные корни. Среди них могут быть и вещественные числа, и мнимые. Пусть 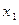 ,
, 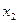 , ¼,
, ¼, 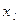 – все вещественные числа в ряду
– все вещественные числа в ряду 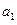 ,
, 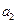 , ¼,
, ¼, 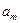 , и пусть
, и пусть 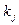 есть кратность
есть кратность 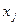 , j = 1, 2, ¼, l. Остальные числа указанного ряда мнимые; в силу теоремы 4 их можно разбить на некоторое количество пар сопряженных друг другу корней. Пусть это будут пары
, j = 1, 2, ¼, l. Остальные числа указанного ряда мнимые; в силу теоремы 4 их можно разбить на некоторое количество пар сопряженных друг другу корней. Пусть это будут пары 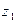 и
и 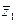 ,
, 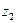 и
и 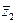 , ¼,
, ¼, 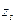 и
и 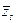 , и пусть
, и пусть 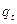 - кратность каждого из корней
- кратность каждого из корней 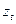 и
и 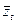 , t = 1, 2, ¼, s. Тогда из (18) получим: " z Î C
, t = 1, 2, ¼, s. Тогда из (18) получим: " z Î C
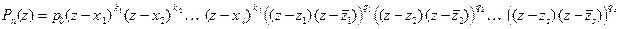
Отсюда: " z Î C
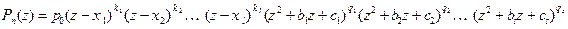 . (19)
. (19)
Это представление вещественного многочлена называют его разложением на вещественные множители, линейные и квадратные. Квадратные множители – это квад- ратные трехчлены с вещественными коэффициентами; каждый из них имеет пару мни -мых сопряженных корней. Справедливо равенство
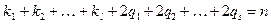 .
.
Пример. Многочлен  , рассмотренный в примере п.2.2, является вещественным многочленом, он имеет простой вещественный корень
, рассмотренный в примере п.2.2, является вещественным многочленом, он имеет простой вещественный корень 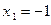 и пару мнимых сопряженных корней
и пару мнимых сопряженных корней 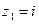 ,
, 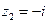 кратности 2. Справедливо представление: " z Î C
кратности 2. Справедливо представление: " z Î C
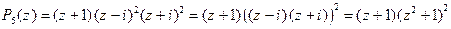 ,
,
так что разложение (19) для 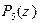 выглядит так:
выглядит так: 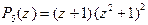 .
.
 2014-02-09
2014-02-09 2743
2743
