Все алгебраические многочлены, рассматриваемые в этом параграфе, являются вещественными многочленами, т.е. их коэффициенты – вещественные числа. Вещественный многочлен 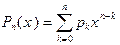 ,
, 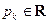 , при вещественных x принимает вещественные значения. Заметим, что такой многочлен может иметь как вещественные, так и мнимые корни.
, при вещественных x принимает вещественные значения. Заметим, что такой многочлен может иметь как вещественные, так и мнимые корни.
3.1 Основные понятия
Функцию 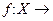 R, заданную равенством
R, заданную равенством 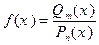 , где
, где 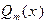 и
и 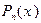 - алгебраические многочлены степени m и n соответственно, называют рациональной функцией.
- алгебраические многочлены степени m и n соответственно, называют рациональной функцией.
Если многочлен 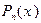 отличен от тождественной константы, т.е. если его сте- пень есть натуральное число, рациональную функцию называют рациональной алгеб- раической дробью или, короче, рациональной дробью. Здесь мы рассматриваем раци- ональные дроби
отличен от тождественной константы, т.е. если его сте- пень есть натуральное число, рациональную функцию называют рациональной алгеб- раической дробью или, короче, рациональной дробью. Здесь мы рассматриваем раци- ональные дроби 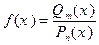 , n ³ 1. В качестве области определения X такой функ- ции выступает вся числовая ось, за вычетом конечного множества точек – веществен- ных корней знаменателя
, n ³ 1. В качестве области определения X такой функ- ции выступает вся числовая ось, за вычетом конечного множества точек – веществен- ных корней знаменателя 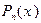 .
.
Рациональную дробь 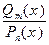 называют правильной, если m < n, и неправиль- ной в противном случае, т.е. когда степень числителя больше или равна степени знаме- нателя. Неправильную рациональную дробь
называют правильной, если m < n, и неправиль- ной в противном случае, т.е. когда степень числителя больше или равна степени знаме- нателя. Неправильную рациональную дробь 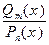 , поделив многочлен
, поделив многочлен 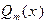 на многочлен
на многочлен 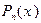 , можно представить в виде суммы алгебраического многочлена и правильной рациональной дроби:
, можно представить в виде суммы алгебраического многочлена и правильной рациональной дроби:
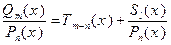 . Здесь
. Здесь 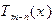 и
и 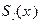 - алгебраические многочлены, причем степень l многочлена
- алгебраические многочлены, причем степень l многочлена 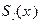 меньше n. Такое преобразование дроби называют выделением её целой части.
меньше n. Такое преобразование дроби называют выделением её целой части.
Элементарными рациональными дробями назовём рациональные дроби следующих двух видов:
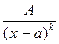 ,
, 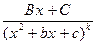 , где A, B, C, a, b, c – вещественные числа, причем
, где A, B, C, a, b, c – вещественные числа, причем 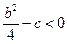 , так что корни трехчлена
, так что корни трехчлена 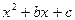 - пара сопряженных мнимых чисел; k – натуральное число.
- пара сопряженных мнимых чисел; k – натуральное число.
3.2. Основная теорема
Пусть 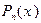 , n ³ 1, – вещественный многочлен степени n, и пусть (19) есть его разложение на вещественные множители. Таким образом,
, n ³ 1, – вещественный многочлен степени n, и пусть (19) есть его разложение на вещественные множители. Таким образом, 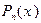 имеет l попарно раз- личных вещественных корней
имеет l попарно раз- личных вещественных корней 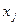 кратности
кратности 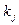 , j = 1, 2,.., l, и s пар мнимых сопря- женных корней
, j = 1, 2,.., l, и s пар мнимых сопря- женных корней 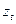 ,
, 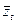 кратности
кратности 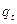 , t = 1, 2,.., s.
, t = 1, 2,.., s.
Теорема 5. ( О разложении правильной дроби в сумму элементарных дробей )
Пусть 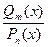 - правильная рациональная дробь (m < n), знаменатель
- правильная рациональная дробь (m < n), знаменатель 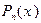 которой представлен разложением (19). Существуют наборы вещественных чисел
которой представлен разложением (19). Существуют наборы вещественных чисел 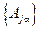 , где j = 1, 2, ¼, l, a = 1, 2, ¼,
, где j = 1, 2, ¼, l, a = 1, 2, ¼, 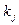 , а также наборы вещественных чисел
, а также наборы вещественных чисел 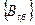 и
и 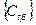 , где t = 1, 2,¼, s, β = 1, 2, ¼,
, где t = 1, 2,¼, s, β = 1, 2, ¼, 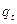 , такие, что при всех x, x Î R,
, такие, что при всех x, x Î R, 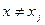 , справед- ливо равенство
, справед- ливо равенство
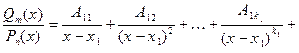
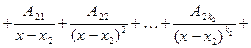
................
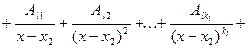
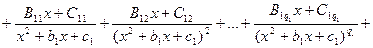
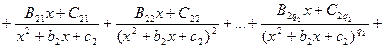
…………………………………………………….
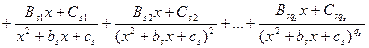 .
.
Доказательство теоремы можно найти в [1].
Замечание. Так как 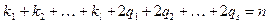 , то общее количество констант
, то общее количество констант 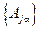 ,
, 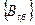 и
и 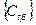 равно степени знаменателя n.
равно степени знаменателя n.
Пример. Дробь 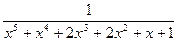 разложим в сумму элементар- ных дробей.
разложим в сумму элементар- ных дробей.
Разложение знаменателя 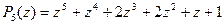 на вещественные множители получено в примере п. 2.3.:
на вещественные множители получено в примере п. 2.3.: 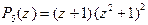 . Многочлен имеет прос- той вещественный корень
. Многочлен имеет прос- той вещественный корень 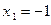 и пару мнимых сопряженных корней
и пару мнимых сопряженных корней 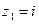 ,
, 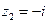 кратности 2. Согласно теореме 5 существуют константы – обозначим их через А, B, C, D, E - такие, что при
кратности 2. Согласно теореме 5 существуют константы – обозначим их через А, B, C, D, E - такие, что при 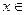 R, х
R, х 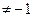
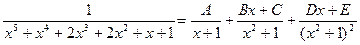 . Найдём эти константы. Приведя дроби в правой части к общему знаменателю, получим равенство между двумя дробями, знаменатели которых одинаковы. Значит, должны совпадать и их числители:
. Найдём эти константы. Приведя дроби в правой части к общему знаменателю, получим равенство между двумя дробями, знаменатели которых одинаковы. Значит, должны совпадать и их числители:
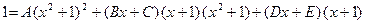 . На это равенство смотрим как на равенство между двумя многочленами, причём сте- пень многочлена в правой части не выше четвёртой. Из равенства и следствия 3 теоре- мы 3 следует, что должны быть одинаковы коэффициенты этих многочленов при оди- наковых степенях х. Приравняв коэффициенты последовательно при
. На это равенство смотрим как на равенство между двумя многочленами, причём сте- пень многочлена в правой части не выше четвёртой. Из равенства и следствия 3 теоре- мы 3 следует, что должны быть одинаковы коэффициенты этих многочленов при оди- наковых степенях х. Приравняв коэффициенты последовательно при 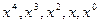 , получим систему уравнений для неизвестных А, B, C, D, E:
, получим систему уравнений для неизвестных А, B, C, D, E:
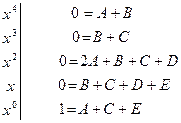
Отсюда: 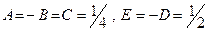 . Итак,
. Итак,
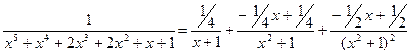 .
.
 2014-02-09
2014-02-09 1388
1388