Обобщение и ограничение

Исключение объема B из объема A – логическая операция, в результате которой образуется новый объем, состоящий из предметов объема A и не состоящий из объема B. Результат этой операции называется логической разностью и обозначается выражением A-B.

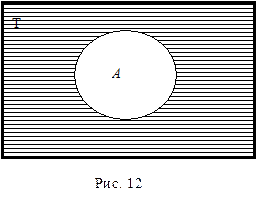
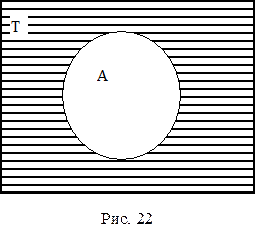
Наконец, дополнение объема A – это логическая операция, в результате которой образуется новый объем, состоящий из предметов универсума Т, не относящихся к объему A. Результат этой операции называется логическим дополнением и обозначается выражением A¢. Дополнением к тыквам весом от 3 до 5 кг будет весь универсум тыкв Т, за исключением тыкв от 3 до 5 кг (рис. 12).

Из приведенных определений видно, что существует соответствие между булевыми операциями и операциями (функторами) логики высказываний. В частности, сложению соответствует слабая дизъюнкция, умножению – конъюнкция, дополнению – отрицание.

Булевы операции подчиняются определенным законам:

AÈA=A	идемпотентность сложения;
AÈВ=ВÈA	коммутативность сложения;
(AÈВ)ÈC=AÈ(BÈC)	ассоциативность сложения;
AÇA=A	идемпотентность умножения;
AÇВ=ВÇA	коммутативность умножения;
(AÇВ)ÇC=AÇ(BÇC)	ассоциативность умножения;
(АÈВ)ÇC=(AÇС)È(BÇC)	Дистрибутивность умножения относительно сложения;

(AÇВ)ÈC=(AÈС)Ç(ВÈC)

Дистрибутивность сложения относительно умножения.

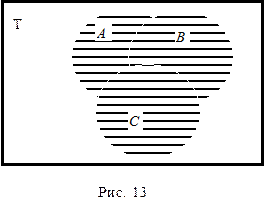
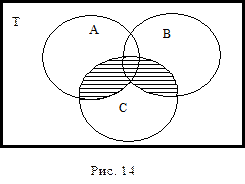
Законы ассоциативности гласят, что в выражениях вида A È В È С и A Ç В Ç С расположение скобок не играет роли, так что их можно вообще опускать (рис. 13 и 14). Однако в таких выражениях, как (A È В)Ç С или A È(В Ç С) – расположение скобок играет существенную роль. Пусть, например, A – объем имени «мужчина», B – объем имени «женщина», С – объем имени «врач». Тогда A È B – объем имени «человек», (A È B)ÇС – объем имени «врач» (рис.15, горизонтальная штриховка); В Ç С – объем имени «женщина-врач», A È(B Ç С) – объем имени, обозначающего всех людей, за исключением женщин, которые не являются врачами (рис. 15, вся штриховка).

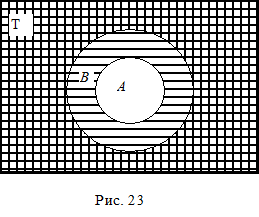
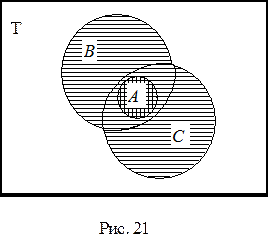
(A B)¢=A¢ Ç B¢ (рис. 24)	- 1-й закон де Моргана
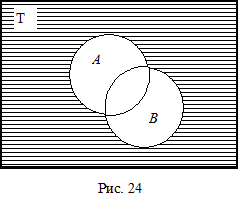
(A Ç B)¢ = A¢ B¢ (рис. 25)	- 2-й закон де Моргана

(A È B)¢=A¢ Ç B¢ (рис. 24);

(A Ç B)¢ = A¢ È B¢ (рис. 25).

В наиболее простых случаях операции обобщения и ограничения можно охарактеризовать следующим образом. Обобщение объема A – логическая операция, в результате которой образуется имя с объемом B, содержащим в себе объем A. Иными словами, обобщить имя A – значит образовать такое другое имя B (род), которое подчиняло бы себе имя A (вид).

Переход от A к B осуществляется за счет отбрасывания признаков, принадлежащих предметам, которые входят в объем A. Так, от имени «вопросительное предложение» переходим к имени «предложение», исключая из первого указание на то, что в грамматической форме этого типа о чем-то спрашивается.

Процессы обобщения – неотъемлемые свойства научного познания. Прежде чем появилось обобщающее имя «закон Бойля-Мариотта», прошли десятилетия упорного труда ученых по исследованию зависимости между давлением и объемом различных газов.

Познавательная роль обобщения состоит, в частности, в том, что признаками родового имени B позволительно наделять любой новый предмет, который оказывается в рамках объема B. Если эта операция производится неверно, то такой перенос ведет к отклонению познания от верного пути. Например, долгое время считалось, что кит является рыбой (это представление закрепилось в разговорных языках ряда народов: русском фольклорном существует «рыба-кит», немецком – “Walfisch” и т.д.). В связи с этим естественны вопросы типа «Что у кита за чешуя?», «Где он мечет икру?» и пр., которые являются тупиковыми.

В процессе познания обобщающее имя в свою очередь может быть обобщено и т.д. Пределом обобщения в каждом конкретном случае выступает некое универсальное имя. В различных науках – это имена, фиксирующие фундаментальные понятия (научные категории): точка, прямая, плоскость – в геометрии; материальная точка, масса, сила, ускорение – в механике; атом, молекула, валентность – в химии; труд, товар, деньги, стоимость – в экономической теории; предмет, свойство, отношение – в логике; право, правовая норма, правовое решение – в юриспруденции.

Ограничение – логическая операция, обратная обобщению. Она состоит в нахождении имени с объемом B, который содержится в объеме A. Ограничить объем A – значит найти такое другое имя B (вид), которое находилось бы в отношении подчинения к A (роду).

Переход от A к B при ограничении осуществляется за счет присоединении признаков, принадлежащих предметам, которые входят в объем A.

Пределом ограничения выступают имена, объемы которых равны одному предмету (единичные имена). Так, пределом ограничения имени «столица» являются имена отдельных государств – Минск, Москва, Токио и т.д.

Особой разновидностью ограничения является выделение типа, или типизация. Тип – это имя, которому однородные предметы соответствуют в той или иной мере. Если некоторые предметы составляют объем имени A и среди них есть такие, которые, безусловно (т.е. со степенью, равной 1), принадлежат к объему B, а другие обладают этим свойством в некоторой (меньшей 1) степени, то имя с объемом B представляет собой тип. Так, ограничивая объем имени «человек», можно получить имя «высокий человек». Это будет тип, поскольку, исходя из практики и разумных соображений, можно выделить, безусловно, высоких людей, остальных же упорядочить по степени их принадлежности к высоким людям, до той границы, за которой находятся, безусловно, невысокие люди (степень их принадлежности к объему имени «высокий человек» равна 0). Тип, таким образом, есть имя с нечетким объемом.

Предметы, которые, безусловно (со степенью, равной 1), принадлежат к объему нечеткого имени, называются типичными представителями данного рода. В концентрированном виде они заключают в себе признаки родственных предметов, служат эталонами их описания и оценки. Например, пан Адольф Быковский в пьесе Я.Купалы “Павлинка” – типичный представитель мелкой белорусской шляхты в начале ХХ века.

Нетрудно видеть, что операции обобщения и ограничения взаимосвязаны. Эта взаимосвязь характеризуется т.н. законом обратного отношения: если имя B является обобщением имени A, а A, очевидно, в этом случае – результат ограничения B, то объем A оставляет правильную часть B, а содержание B является частью содержания B.

Уместен вопрос: что произойдет с объемом имени (соответственно с его содержанием), если он пополнится новыми предметами со своими специфическими свойствами? Увеличится ли, например, объем имени «химический элемент» в связи с открытием нового химического элемента? Произойдут ли при этом изменения в содержании этого имени? На эти вопросы следует ответить отрицательно. Объем имени «химический элемент», как и его содержание, остается стабильным. Ведь признак, в соответствии с которым этот объем выделяется и фиксируется («простое вещество, неразложимое обычными химическими методами на части»), остается неизменным.

Присоединение к объему новых предметов, тождественных со старыми по некоторому признаку, называется логической операцией расширения объема A.

Операция, обратная расширению, т.е. удаление из объема A предметов, которые тождественны с оставшимися по некоторым признакам, называется локализацией объема имени A. Примером локализации может служить произведенное в свое время в биологии удаление китов из класса рыб, хотя объем и содержание имени «рыба» остался неизменным.

Логические операции с объемами имен не следует смешивать с мысленными переходами от части к целому и, наоборот, от целого к части. Специфика последних наиболее отчетливо выявляется при их сопоставлении с операциями обобщения и ограничения.

Обобщаемое имя заключает в себе все содержание результата обобщения, но не наоборот. Иными словами, вид обладает всеми признаками рода. Например, можно, обобщив имя «газета», получить имя «периодическое издание», и ни одна газета не мыслима без этого родового признака.

Иначе обстоит дело при переходе от части к целому. Ознакомившись с отдельными помещениями в новой квартире, можно составить представление о квартире в целом, но нельзя переносить свойства всей квартиры (например, то, что она состоит из трех комнат), на каждую из частей квартиры. Часть, таким образом, не обладает содержанием целого. Поэтому смешение операции обобщения (ограничения) с операцией мысленного перехода от части к целому (от целого к части) непозволительно и может служить источником серьезных заблуждений. Например, восточнославянское племя кривичей можно рассматривать иногда как разновидность, иногда как часть славян. В первом случае, зная, что восточные славяне поклонялись Перуну, мы не сделаем ошибки, заключив, что и кривичи поклонялись Перуну (операция ограничения). Во втором же случае из знания о том, что восточные славяне подвергались набегам степняков, вовсе не следует, что и любая их часть, например, кривичи подвергались этим набегам (переход от целого к части). В противном случае допускается логическая ошибка.

Операции обобщения и ограничения играют большую роль в правовой науке. В частности, выделяя из многих понятий общие признаки, формируют понятия, которые являются более широкими по своему объему. Путем установления общих признаков понятий «вор», «убийца», «взяточник» и др., а именно того, что они являются нарушителями диспозиции нормы и субъектами, по отношению к которым в принципе должна применяться санкция, образуется понятие «правонарушитель». Соответственно сформированы такие понятия, как «субъект права», «нормативный акт» и пр.

При ограничении от понимания родового имени во многом зависит трактовка всякого видового имени. Например, зная, какие признаки входят в содержание имени «преступление» («деяние», «общественно-опасное», «противоправное»), можно с уверенностью утверждать, что и «грабеж», как вид преступления, также обладает этими (но не только этими) признаками.

Логика соотношения целого и части находит отражение, например, в статье 52 Гражданского кодекса Республики Беларусь: «Учредители (участники) юридического лица или собственник его имущества не отвечает по обязательству юридического лица, а юридическое лицо не отвечает по обязательствам учредителя (участника) или собственника, за исключением случаев, предусмотренных законодательством либо документами юридического лица».

Упражнения:

1. Найдите сумму объемов A и B (A È B) в каждом из следующих случаев:

a) поэт (A), прозаик (B);

b) внешнеэкономическая деятельность (A), международная торговля (B);

c) четное натуральное число (A), нечетное натуральное число (B);

d) последняя буква русского алфавита (A), тридцать третья буква русского алфавита (B);

e) король (A), нынешний король Польши (B).

2. Найдите произведение объемов A и B (A Ç B) из упр.1.

3. Пусть множество людей – универсальный объем Т. Сформулируйте результаты дополнения объемов следующих имен:

a) мужчина;

b) несовершеннолетний;

c) человек ростом 180 см. и выше;

d) человек, родившийся на Луне;

e) человек с мягкой мочкой уха.

4. Какие из следующих имен обобщаются именем «правильная дробь»:

a) дробь, в которой числитель меньше знаменателя;

b) натуральное число;

c) знаменатель;

d) 1/2;

e) 4/3;

f) дробь со знаменателем, равным нулю?

5. Какие из следующих имен можно ограничить, какие – нет:

a) полюс Земли;

b) созвездие Большой Медведицы;

c) Вселенная;

d) пространство (в геометрии);

e) тело (в механике)?

6. Какие имена из упр.9 можно обобщить, какие – нет?

7. В каких из следующих случаев имеет место логическая операция ограничения имени A:

a) минута (A) – секунда (B);

b) часть минуты (A) – секунда (B);

c) часть минуты (A) – часть секунды (B);

d) секунда (A) – часть секунды (B)?

8. Какое требование логики игнорирует автор следующего высказывания: «Если каждый человек рискует, то и все человечество рискует» (Ж.-П. Сартр).

9. Пусть A – объем имени «мужчина», B – объем имени «юноша», C – объем имени «мужчина не старше 50 лет». Что будут означать выражения:

a) A Ç(B Ç C);

b) A È(B È C);

c) A Ç(B È C);

d) A È(B Ç C)?

10. Пусть множество ученых – универсальный объем Т, а также: A – объем имени «античный ученый», B – объем имени «современный ученый», С – объем имени «физик», D – объем имени «Эйнштейн». Сформулируйте имена, имеющие объемы:

a) (A Ç D)¢È B;

b) (B È C)¢Ç D;

c) (B È C ¢)Ç D;

d) (Т — A) Ç C;

e) (A ' — Т) È A;

f) Т — (A Ç B).

11. Из 50 учеников, сдавших экзамены по физике и математике, физику успешно сдали 45, математику – 44, физику и математику – 40. Сколько учеников провалило оба экзамена?