2014-02-09
1887
Определим анодный и сеточный токи в лампе графическим методом по аппроксимированным характеристикам. При выполнении построений принято во внимание, что анодный ток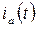 
протекает только при мгновенном значении напряжения на управляющей сетке 
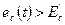а сеточный 
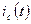- при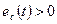 
. При остальных значениях напряжения 
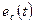эти токи равны нулю. В результате анодный и сеточный токи приобретают форму импульсов косинусоидальной формы.
Эти импульсы характеризуются амплитудой и длительностью у основания, половина которой называется углом отсечки. Импульсы анодного тока имеют амплитуду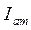 
и угол отсечки 
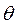, импульсы сеточного тока - 
, 
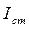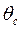. Такие импульсы периодически повторяются через 
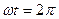. Таким образом, в анодной цепи лампы протекает ток 
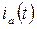импульсной формы, а в сеточной - ток 
.
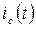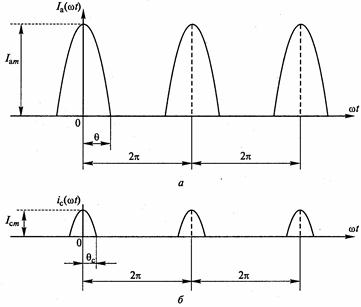
Проведем ось ординат посредине первого косинусоидального импульса. Тогда для анодного тока при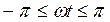 
запишем: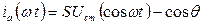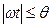 
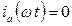при 
; 
, при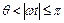 
,
где S - крутизна анодно-сеточной характеристики;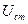 
- амплитуда входного сигнала.
Из 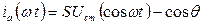при 
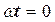получим для амплитуды анодного тока
.
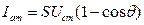Косинус угла отсечки анодного тока
.
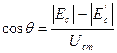Аналогично для сеточного тока при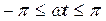 
запишем:
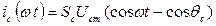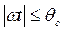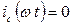при 
;
при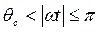 
.
Из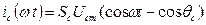 
при 
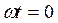получим для амплитуды сеточного тока
.
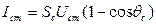Косинус угла отсечки сеточного тока
.
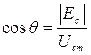Разложим периодическую функцию 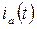в ряд Фурье
,
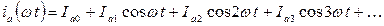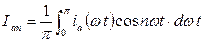- n-я гармоника анодного тока, где n=0,1, 2, 3...
Вычислив интеграл, получим для постоянной составляющей анодного тока с учетом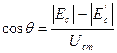
.
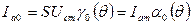где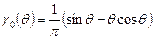 
; 
.
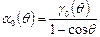Для n-й гармоники анодного тока с учетом
,
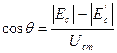
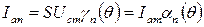где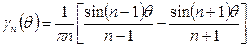 
; 
.
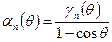Для 1-й гармоники (n=1) имеем
,
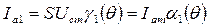где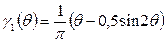 
; 
.
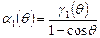Коэффициент формы косинусоидального импульса:
.
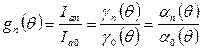Зависимости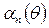 
, 
, 
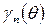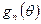называются коэффициентами разложения в ряд Фурье косинусоидальных импульсов.
Аналогично производится разложение в ряд импульсов сеточного тока:
;
.
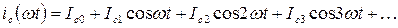
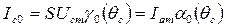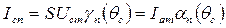Определим напряжение на анодном контуре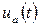 
.
При настройке контура в резонанс (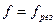
) он имеет большое сопротивление на частоте 1-й гармоники:
,
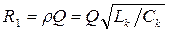где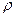 
- волновое сопротивление контура и малое, близкое к нулю, на всех остальных гармониках - 2, 3-й и т.д. Такое свойство контура позволяет считать напряжение на нем синусоидальным
,
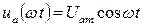где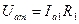 
- амплитуда напряжения 1-й гармоники на контуре.
Для напряжения между электродами лампы анод-катод имеем
.
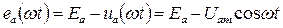Согласно полученным выражениям для напряжений на управляющей сетке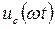 
и аноде 
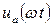и для анодного 
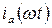и сеточного токов 
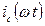построим соответствующие диаграммы, отображающие формы сигнала на выходе и входе электронного прибора ВЧ генератора.
Полученные выражения позволяют составить уравнения баланса мощностей в генераторе.
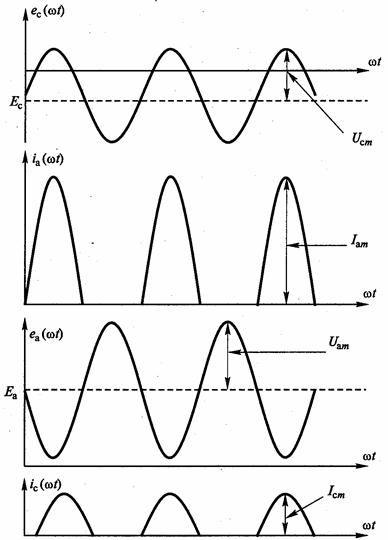
Уравнение баланса мощностей в анодной цепи генератора примет вид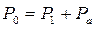 
,
где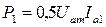 
мощность 1-й гармоники сигнала в анодной цепи или выходная мощность ВЧ генератора;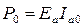 
мощность, потребляемая от источника постоянного тока по цепи анода;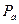 
- мощность, рассеиваемая в виде тепла анодом лампы.
Для КПД генератора получим
,
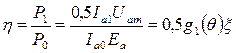где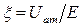 
- коэффициент использования анодного напряжения.
Уравнение баланса мощностей в сеточной цепи ВЧ генератора примет вид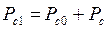 
,
где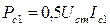 
,
мощность 1-й гармоники сигнала в сеточной цепи или входная мощность ВЧ генератора;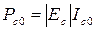 
мощность, рассеиваемая в источнике напряжения смещения;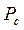 
- мощность, рассеиваемая в виде тепла управляющей сеткой лампы. Значения 
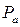и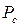 
не должны превышать предельных значений данных параметров в используемом электровакуумном приборе.
