Задание для самостоятельной работы
Выводы.
На основе проведенного анализа сложного периодического сигнала можно сделать следующие выводы:
· датчик, установленный в какой-либо точке исследуемой механической системы, измеряет функцию времени в виде
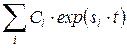 ; ;
|
· функция времени имеет стандартный вид: 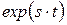 ;
;
· вибрация механической системы есть суперпозиция гармонических колебаний и затухающих собственных колебаний (с демпфированием);
· любой периодический сигнал может быть представлен в виде суммы простых гармоник.
Разложить в сумму простых гармоник приведенные ниже периодические функции.
Представить графически приближение периодической функции суммой гармоник в зависимости от числа приближений.
Построить график изменения гармонического сигнала в зависимости от номера гармоники.
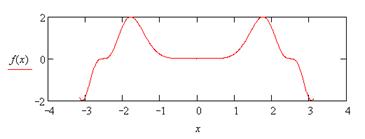
| № | Функция | Интервал | График |
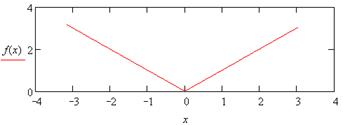
| 1. | 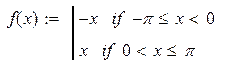
| 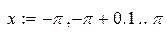
| 
|
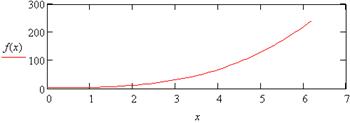
| 2. | 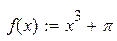
| 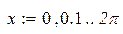
| 
|
| 3. | 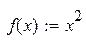
| 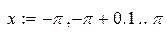
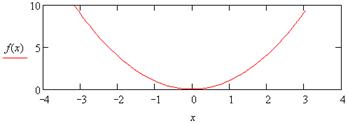
| 
|
| 4. | 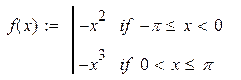
| 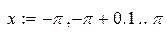
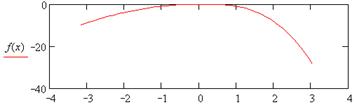
| 
|
| 5. | 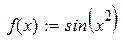
| 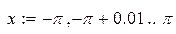
| 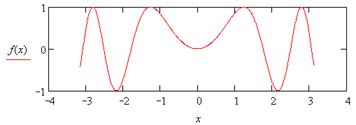
|
| 6. | 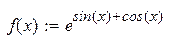
| 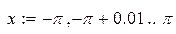
| 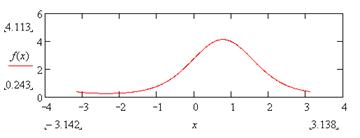
|
| 7. | 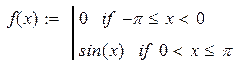
| 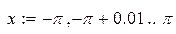
| 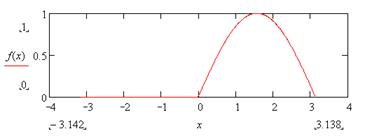
|
| 8. | 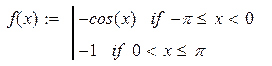
| 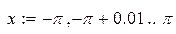
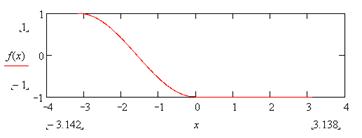
| 
|
| 9. | 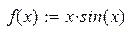
| 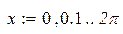
| 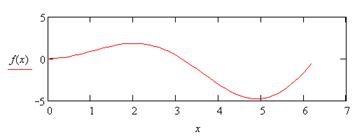
|
| 10. | 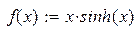
| 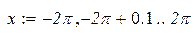
| 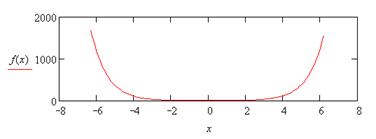
|
| 11. | 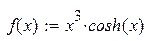
| 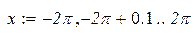
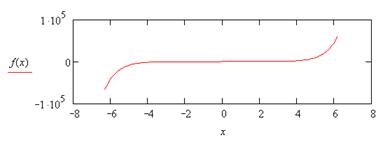
| 
|
| 12. | 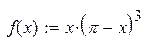
| 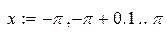
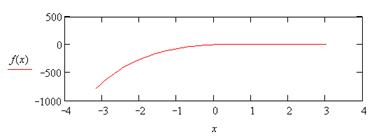
| 
|
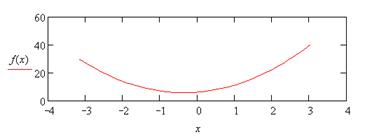
| 13. | 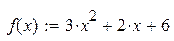
| 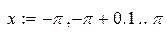
| 
|
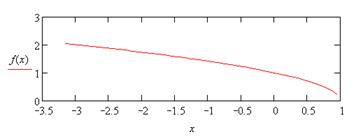
| 14. | 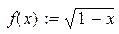
| 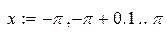
| 
|
| 15. | 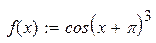
| 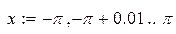
| 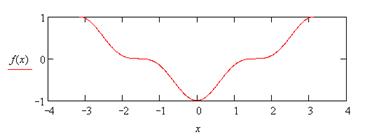
|
| 16. | 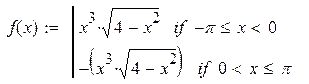
| 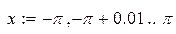
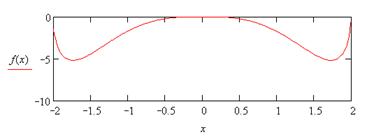
| 
|
| 17. | 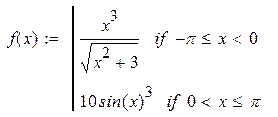
| 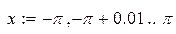
| 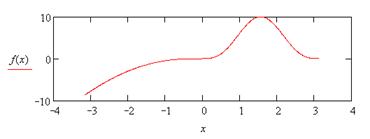
|
| 18. | 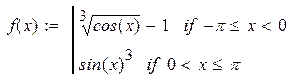
| 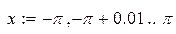
| 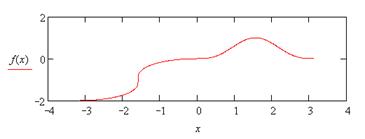
|
| 19. | 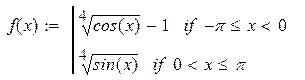
| 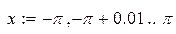
| 
|
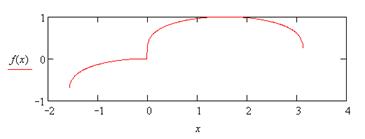
| 20. | 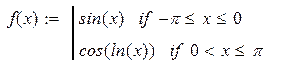
| 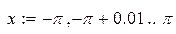
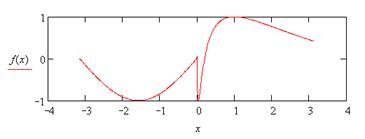
| 
|
| 21. | 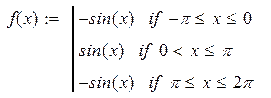
| 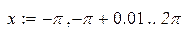
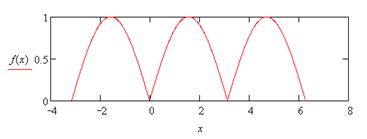
| 
|
| 22. | 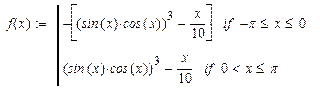
| 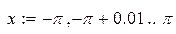
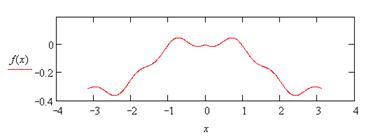
| 
|
| 23. | 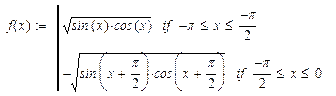
| 
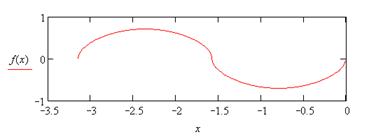
| 
|
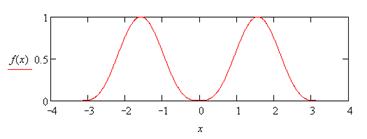
| 24. | 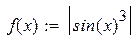
| 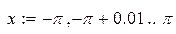
| 
|
| 25. | 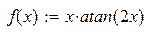
| 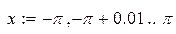
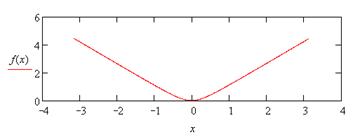
| 
|
| 26. | 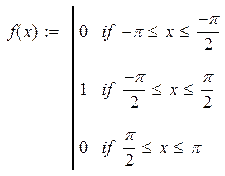
| 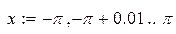
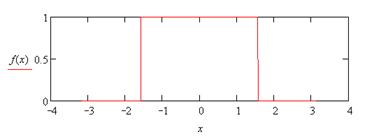
| 
|
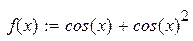
| 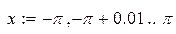
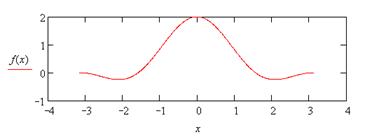
| 
| |
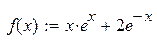
| 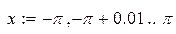
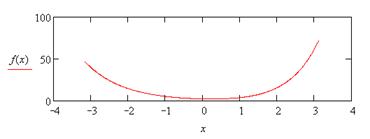
| 
| |
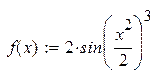
| 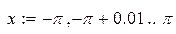
| 
|
 2014-02-17
2014-02-17 490
490








