Атомы
Выражение предикатный_символ (терм, терм,..., терм) называют атомом. Атом представляет предикат. Особо выделяется атом, предикатным символом которого является знак равенства, а аргументами два терма. Этот атом можно было бы представить как равны (терм, терм) или= (терм, терм), но, как правило, его записывают в обычной инфиксной форме терм = терм. Этот атом истинен, когда значения обоих термов совпадают. Атомы без знака отрицания или со знаком отрицания называют литералами.
Когда мы имеем дело с объектами, то возникает естественная потребность выразить какие-либо общие свойства целого множества объектов. Кванторы как раз служат этим целям. Таких кванторов в логике предикатов всего два.
Квантор общности 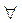 . Вспомним, что при решении задачи поиска золота в среде чудовища для того, чтобы выразить правило "В какой бы ячейке агент не находился, если он видит блеск золота, то он должен его взять", было использовано 16 однотипных формул (2.8), число которых совпадает с числом ячеек. Эти формулы имели вид
. Вспомним, что при решении задачи поиска золота в среде чудовища для того, чтобы выразить правило "В какой бы ячейке агент не находился, если он видит блеск золота, то он должен его взять", было использовано 16 однотипных формул (2.8), число которых совпадает с числом ячеек. Эти формулы имели вид
xн(1, 1) 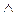 х6(1, 1)
х6(1, 1) 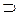 z3,
z3,
…
xн(i, j) 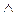 х6(i, j)
х6(i, j) 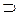 z3, (3.1)
z3, (3.1)
…
xн(4, 4) 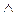 х6(4, 4)
х6(4, 4) 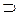 z3.
z3.
Здесь xн(i, j), x6(i, j) — отдельные переменные. Каждая из них принимает истинное значение, если соответствующий ей объект (в данном случае агент и золото, точнее блеск золота) находится в ячейке (i, j), Обратим еще раз внимание на то, что xн(i, j) и x6(i, j)) — это индексированные логические переменные с индексами н, б, i, j, каждая из которых считается единым неделимым символом. Большое количество формул пришлось вводить из-за того, что в логике высказываний нет возможности представить указанное выше правило в виде одной формулы. В логике предикатов такая возможность имеется и, вместо 16 формул в логике высказываний, в логике предикатов можно написать одну:
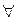 (i,j) xн(i, j)
(i,j) xн(i, j) 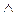 х6(i, j)
х6(i, j) 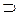 z3, (3.2)
z3, (3.2)
где знак 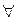 называется квантором общности. Но в этой формуле xн(i, j),х6(i, j) и z3 неявляются логическими переменными. Здесь хн, х6, z, — предикатные символы, вид которых для удобства сохранен тем же, что и в логических переменных, а i, j — числовые объектные переменные, соответствующие координатам ячеек. На естественном языке это правило формулируется следующим образом: "Для всех ячеек с координатами (i, j) справедливо: если агент находится в ячейке с координатами (i, j) и видит в ней блеск золота, то он должен его взять".
называется квантором общности. Но в этой формуле xн(i, j),х6(i, j) и z3 неявляются логическими переменными. Здесь хн, х6, z, — предикатные символы, вид которых для удобства сохранен тем же, что и в логических переменных, а i, j — числовые объектные переменные, соответствующие координатам ячеек. На естественном языке это правило формулируется следующим образом: "Для всех ячеек с координатами (i, j) справедливо: если агент находится в ячейке с координатами (i, j) и видит в ней блеск золота, то он должен его взять".
Смысл квантора общности V совпадает с выражением естественного языка "Для всех...". Множество формул (3.1) логики высказываний эквивалентно одной формуле (3.2) логики предикатов, т.е имеет место
(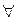 (i, j) xH(i, j)
(i, j) xH(i, j) 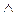 х6(i, j)
х6(i, j) 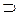 z3)
z3) 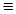 (xн(1, 1)
(xн(1, 1) 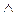 х6(1, 1)
х6(1, 1) 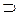 z3)
z3) 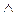 (хн (1, 2)
(хн (1, 2) 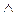 х6(1, 2)
х6(1, 2) 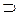 z3)
z3) 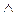 (хн (4, 4)
(хн (4, 4) 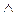 х6(4, 4)
х6(4, 4) 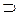 z3).
z3).
Квантор существования 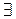 . Квантор общности позволяет формулировать высказывания о свойствах целого множества объектов. В то же время часто возникает необходимость высказываться о свойствах отдельных объектов из какой-либо их совокупности. Для этого используют квантор существования 3. Вернемся к примеру со средой чудовища. Во второй главе для того, чтобы выразить знания о наличии чудовища в ячейках, соседних ячейке с координатами (i,j), если в ней ощущается зловоние, было введено 16 формул, в которых индексы i, j пробегают множество значений от 1 до 4. Вместо этих 16 формул с помощью квантора общности можно записать одну формулу, помня, что теперь вместо логических переменных используются предикаты, а индексы стали числовыми объектными переменными:
. Квантор общности позволяет формулировать высказывания о свойствах целого множества объектов. В то же время часто возникает необходимость высказываться о свойствах отдельных объектов из какой-либо их совокупности. Для этого используют квантор существования 3. Вернемся к примеру со средой чудовища. Во второй главе для того, чтобы выразить знания о наличии чудовища в ячейках, соседних ячейке с координатами (i,j), если в ней ощущается зловоние, было введено 16 формул, в которых индексы i, j пробегают множество значений от 1 до 4. Вместо этих 16 формул с помощью квантора общности можно записать одну формулу, помня, что теперь вместо логических переменных используются предикаты, а индексы стали числовыми объектными переменными:
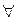 (i,j) xз(i,j)
(i,j) xз(i,j) 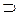 xч(i,j)
xч(i,j) 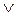 xч(i-1,j)
xч(i-1,j) 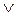 xч(i+1,j)
xч(i+1,j) 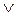 xч(i,j-1)
xч(i,j-1) 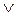 xч(i,j+1). (3.3)
xч(i,j+1). (3.3)
На естественном языке высказывание, соответствующее этой формуле, звучит так: "Для всех ячеек с координатами (i,j) справедливо: если ощущается зловоние в ячейке с координатами (i,j), то существует ячейка, соседняя ячейке с координатами (i,j), в которой находится чудовище". Для того чтобы выразить часть этого высказывания "...существует ячейка, соседняя ячейке с координатами (i,j), в которой находится чудовище" в логике высказываний были использованы формулы, в которых справа от знака импликации стоит дизъюнкция пяти логических переменных. В логике предикатов имеется возможность более короткой записи этой части высказывания с использованием квантора существования 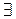 :
:
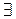 (g, h) xч{g, h)
(g, h) xч{g, h) 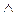 ((g = i
((g = i 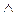 (h =j-1
(h =j-1 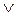 h = j +1)
h = j +1) 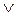 (h = j
(h = j 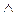 (g = i-1
(g = i-1 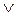
g = i+1)).
Используя эту запись вместо 16 формул логики высказываний, в логике предикатов можно ограничиться одной формулой (3.4)
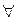 (i, j) хз(i, j)
(i, j) хз(i, j) 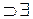 (g, h) xч(g, h)
(g, h) xч(g, h) 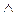 ((g = i
((g = i 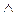 (h = j -1
(h = j -1 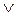 h =j +1)
h =j +1) 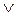
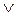 (h = j
(h = j 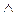 (g = i-1
(g = i-1 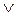 g = i+1)) (3.4)
g = i+1)) (3.4)
Квантор существования произносится на естественном языке как "Существует...".
Взаимосвязь между кванторами. Считают, что квантор связывает переменные, которые записываются за знаком квантора в скобках. Поэтому их называют связанными. Переменные же, которые ни один квантор не связывает, называют свободными. Взаимосвязь между кванторами существования и общности можно легко выразить с помощью связки -i и она основана на следующем соображении: если какая-либо совокупность переменных связана квантором общности таким образом, что все объекты, которым соответствуют эти переменные, не обладают каким-то общим свойством, то не существует объекта (а следовательно, и соответствующей ему переменной), который обладал бы этим свойством. Например, в случае среды чудовища, если во всех ячейках нет чудовища, то это означает, что не существует ни одной ячейки, в которой бы находилось чудовище и наоборот. Эту взаимосвязь можно описать следующей формулой:
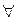 (i,j)
(i,j)  xч(i,j)
xч(i,j) 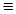

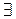 (i,j) хч(i,j).
(i,j) хч(i,j).
Если же ямы находятся во всех ячейках, то это означает, что не существует ячейки, в которой не было бы ямы. Эту взаимосвязь можно выразить формулой
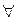 (i,j)xя(i,j)
(i,j)xя(i,j) 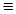

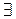 (i,j)
(i,j)  хя(i,j).
хя(i,j).
Продолжая аналогичные рассуждения и обозначая Р(х) любую формулу, переменная х которой связана кванторами, получаем следующие законы, характеризующие взаимосвязь между кванторами:
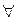 (x)
(x)  P(x)
P(x) 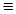

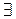 (x)P(x),
(x)P(x),

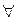 (x)P(x)
(x)P(x) 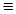
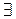 (x)
(x)  P(x),
P(x),
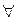 (x)P(x)
(x)P(x) 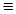

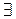 (x)
(x)  P(x),
P(x),

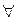 (x)
(x)  P(x)
P(x) 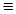
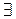 (x)P(x).
(x)P(x).
 2014-02-09
2014-02-09 2539
2539








