Рассмотрим в начале работу цифрового тракта. 8 страница

Ясно, что рассматриваемая задача сводится к задаче выбора матриц F_i, G_i и H_i для каждой i-й локальной системы, входящей в состав распределенной. При этом предлагается пойти по следующему пути. Специальными приемами свести рассмотрение информационных графов произвольного вида к анализу некоторых стандартных (примитивных) графов, а именно, цепей. Итак, при построении модели распределенной системы воспользуемся следующим алгоритмом. По информационному графу найдем множество путей, составляющих покрытие его ребер. Под путем понимается последовательность ребер и вершин, соединяющая некоторый вход информационного графа с его выходом. Для рассматриваемого примера (рис. 5.8) покрытие обеспечивается двумя путями с ребрам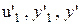и и 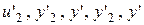. Здесь штрихи используются для обозначения передаваемой в массивах тестовой информации. Второй путь содержит цикл для покрытия информационной обратной связи с выхода распределенной системы на вход локальной системы F₂. Сопоставим в модели распределенной системы с каждым путем цепь из такого числа динамических звеньев M, через сколько локальных систем проходит данный путь. При этом, если в путь входит i-я локальная система, и она является j-й по порядку в этой цепи, то с ней сопоставляется звено 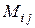. На рис. 5.10. представлена модель для распределенной системы из рассматриваемого примера. При этом модель первой локальной системы содержит одно звено 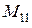, модель второй системы – два звена 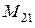и 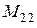, а модель третьей системы – три звена 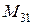, 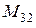и 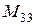. Каждое звено обрабатывает информацию лишь от одного массива и по одному и тому же алгоритму, поэтому оно описывается стационарными уравнениями. В отличие от звена локальная система в общем случае обрабатывает несколько массивов, а, следовательно, ее модель содержит параллельную композицию нескольких звеньев, срабатывающих в разные моменты времени и обрабатывающих информацию в общем случае по разным алгоритмам. Это означает, что модель локальной системы нестационарна. Передаваемые массивы имеют разную размерность, определяемую количеством и структурой звеньев, составляющих модель конкретной локальной системы.

Отметим важнейшую особенность структуры массива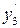, выдаваемого из третьей системы. В ней можно выделить две части, одна из которых формируется в звеньях 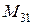и 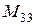и предназначена для средств диагностирования, другая формируется в 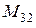и предназначена для второй системы.

Таким образом, можно сказать, что результат алгоритма формируется как массив значений аргументов, подвергнувшихся независимой обработке.

После описанных построений модель представляется совокупностью независимых цепей. Очевидно, что для ее наблюдаемости и управляемости необходимо и достаточно, чтобы каждая из цепей была наблюдаема и управляема. Таким образом, задача синтеза наблюдаемой и управляемой модели распределенной системы свелась к синтезу наблюдаемой и управляемой цепи. Последняя задача гораздо проще предыдущей.

Прежде чем переходить к синтезу цепей, обсудим одно усложняющее задачу обстоятельство. Обычно при обсуждении задач наблюдения и управления предполагается непрерывность этих процессов во времени (если система дискретная, то наблюдение и управление осуществляется во всех тактах). Для рассматриваемой задачи во многих практических случаях это условие не выполняется, поскольку наблюдение осуществляется лишь в сеансах пересылки информации из выходной системы в средства диагностирования, а управление - в сеансах пересылки информации из средств диагностирования во входные системы. Зачастую таких сеансов всего два за период – по одному на наблюдение и управление. Поэтому в дальнейшем нас интересуют свойства наблюдаемости и управляемости относительно ограниченного числа точек наблюдения и управления. Задача обеспечения полной наблюдаемости и управляемости сильно упрощается, если матрицы 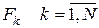модели распределенной системы неособенные. Действительно, пусть в этом случае модель 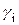-наблюдаема и 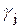-управляема. 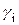-наблюдаемость модели позволяет определить по ее выходу состояние 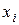, в котором система находится в момент времени, совпадающий с началом последовательности 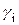. В каждом периоде такой момент один. Однако благодаря неособенности матриц 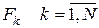можно, зная 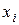, определить не только любое последующее, но и любое предыдущее состояния. Этот факт свидетельствует о полной наблюдаемости системы. Очевидно, что аналогичный вывод справедлив и относительно управляемости. В результате приходим к утверждению, что периодически нестационарная система полностью наблюдаема и управляема, если она 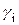-наблюдаема, 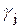-управляема, а ее матрицы 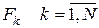- неособенные.

Для того чтобы в описываемой модели матрицы сеансов были неособенными, необходимо и достаточно выбрать неособенными матрицы динамики диагностических алгоритмов локальных систем.

Будем считать, что любое звено, принадлежащее r-й цепи выдает и принимает информацию лишь один раз за период расписания цепи. Цепи могут быть однородными (содержащими лишь одинаковые звенья) и неоднородными. Ниже рассматривается второй, более общий случай, а точнее, два в определенном смысле крайних варианта. В первом из них цепь состоит из звеньев (назовем их векторными) с входными и выходными векторами максимальной размерности, равной размерности m звена, во втором случае – из скалярных звеньев. Первый случай характеризуется максимумом информации, передаваемой за период в целях диагностирования, второй – минимумом. Однако в первом случае максимальны индексы наблюдаемости и управляемости и, как следствие, длина теста, а во втором случае – эти показатели минимальны. Предположим, что в обоих случаях все звенья наблюдаемы и управляемы, а во втором случае к тому же реализованы в строчной наблюдаемой форме [1] причем m > 1, т.е.:

, ,

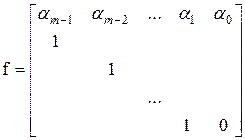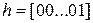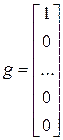
где 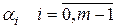- коэффициенты характеристического многочлена матрицы f (здесь и далее матрицы в описании звеньев обозначаются маленькими буквами).

Тогда справедливо утверждение: цепь, составленная из q векторных звеньев одинаковой размерности 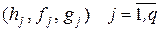полностью наблюдаема и управляема при любом расписании, если матрицы 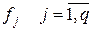неособенные.

То же самое утверждение, но относительно цепи из скалярных звеньев требует выполнения более жестких условий:

1. характеристические многочлены 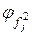матриц 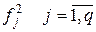- неприводимы;

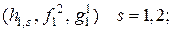
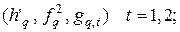
2. скалярные звенья 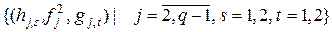, где 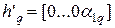; ; 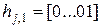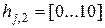, , 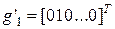, , 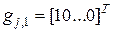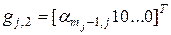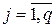- наблюдаемые и управляемые.

Ужесточение требований к звеньям в скалярном случае объясняется ухудшением наблюдаемости и управляемости звеньев (особенностями их входных и выходных матриц). Появление в условиях 1 и 2 квадратов матриц 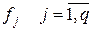связано с предположением о двукратном срабатывании звеньев за период цепи. В обоих рассмотренных случаях утверждается независимость от расписания обмена в цепи. Кстати, именно эта деталь определяет громоздкость условия 2. Указанное свойство существенно для практики проектирования средств диагностирования, поскольку в этом случае неизбежные трансформации расписания обмена в процессе проектирования не влияют на их диагностическую модель.

Для примера выберем звенья для модели на рис. 5.10. В данном случае модель может быть построена из однородных цепей. Пусть цепи образованы скалярными звеньями. Выберем для всех цепей следующую структуру звена:

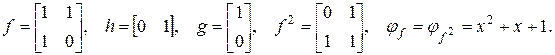
Проверим выполнение условий 1 и 2. Многочлен 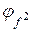неприводим (условие 1 выполняется). Для проверки условия 2 убедимся, что звенья с матрицей 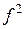наблюдаемы при выходных матрицах:

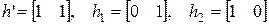
и управляемы при входных матрицах:

.

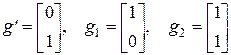Вычислим для всех этих случаев матрицы наблюдаемости W и управляемости P:

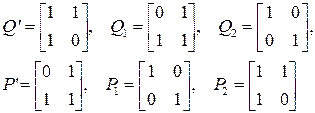
Очевидно, что все матрицы неособенные, а, следовательно, условие 2 выполняется.

Вопросы

1. Тестовое диагностирование безынерционных устройств

2. Тестовое диагностирование динамических устройств

3. Тестовое диагностирование дискретных устройств. Общий подход.

4. Тестовое диагностирование линейных дискретных устройств. Структурный подход.

5. Тестовое диагностирование линейных дискретных устройств. Абстрактный подход.

6. Тестовое диагностирование аналоговых линейных устройств.

7. Тестовое диагностирование мультирежимных систем.

8. Тестовое диагностирование процессора.

9. Тестовое диагностирование распределенных информационно-управляющих систем. Построение проверяющего теста. Управляемость и наблюдаемость периодически нестационарной системы.

10. Тестовое диагностирование распределенных информационно-управляющих систем. Синтез модели системы обмена.

6. Методы функционального диагностирования

В данном разделе излагаются методы функционального диагностирования. При этом ни в кое случае не ставится цель исчерпывающего изложения известных методов ФД. Фактически приводятся лишь краткие сведения из этой области, по которым, по нашему мнению, можно составить представление о возможностях некоторых известных подходов. Задача рассматривается лишь для систем, описываемых динамической моделью. В мировой литературе задача ФД в научном плане рассматривается только для таких систем. Это, по-видимому, объясняется тем, что для более простых и более сложных систем в решении задачи ФД нет практической целесообразности.

В настоящее время в функциональном диагностировании известны два основных подхода - детерминированный и стохастический. Первый использует детерминированную модель диагностируемой системы, второй – стохастическую. Однако наряду с ними или в их рамках существуют направления, может быть, менее значимые по числу публикаций и основанные на нечетких или интервальных моделях. Возможны и смешанные, в частности, интервально-стохастические подходы. Выбор того или иного подхода, как правило, определяется содержанием априорной информации о свойствах системы и возникающих в ней отказах, имеющейся в распоряжении разработчика средств диагностирования. Так если разработчик располагает статистической информацией о поведении системы и ее отказах, то может быть применен стохастический подход. Если такой информации нет, то применяется детерминированный подход. Безусловно, между методами, соответствующими различным подходам, можно заметить определенную аналогию. Она является следствием взаимного проникновения и обогащения существующих подходов. Практически весь приводимый далее материал (за исключением последнего подраздела) соответствует детерминированному подходу.

Решение задачи ФД рассматривается как в отношении линейных, так и в отношении нелинейных динамических систем. При этом используются модели (5.4) – (5.6). Перед тем как перейти к обсуждению конкретных методов хочется еще раз напомнить о необходимости описания при построении средств диагностировании класса отказов, на которые нацелены эти средства. Без этого невозможно на завершающем этапе проектирования определить, какого же качества оказались полученные средства диагностирования, соотнеся список реально охваченных диагностированием отказов с первоначально намеченным списком.

6.1. Методы функционального диагностирования для обнаружения отказов

В данном подразделе в обзорном плане описываются методы обнаружения отказов. Эта задача существенно проще, нежели задача поиска отказов, когда требуется не просто забраковать диагностируемую систему как неработоспособную, но и с необходимой точностью определить местоположения отказа. Методы поиска отказов будут рассмотрены в последующих подразделах.

В рамках детерминированного подхода можно выделить определенные направления. При этом основными среди них можно считать направления, основанные на использовании алгебраических инвариантов [20], соотношений паритета, моделей объекта диагностирования [5, 8, 10, 24 – 29, 33].

Инвариант – это в данном случае некоторая характеристика объекта, сохраняющая свое значение для работоспособного объекта и изменяющая это значение при его отказе. При этом функция СД состоит в вычислении значения используемого инварианта и в сравнении этого значения с эталоном (рис. 6.1). При поиске отказов необходимо, чтобы разным отказам соответствовали бы разные значения инварианта. В качестве инвариантов могут выступать, например:

­ полюса передаточной функции;

­ элементы системных матриц;

­ значения частотных характеристик на фиксированных частотах;

­ отсчеты импульсной и переходной функций в фиксированные моменты времени.

Второе направление иллюстрируется на рис.6.2, где предполагается, что диагностируемая система линейна и описана в операторной форме. Видно, что в этом случае невязка формируется при сопоставлении преобразованных входа u и выхода y системы.

Наконец, третье направление предполагает, что невязка формируется при сопоставлении выходов диагностируемой системы и ее модели, которая может формироваться на компьютере. Простейшая иллюстрация этого подхода приведена на рис. 6.3, где предполагается, что система и ее модель, стартуя из одинаковых состояний, формируют при номинальном поведении совпадающие последовательности выходов, а при появлении отказов в системе эти последовательности расходятся (генерируется ненулевая невязка r).

В рамках этого направления предложен целый ряд методов, ориентированных как на обнаружение отказов, так и на их поиск. Причем могут рассматриваться как линейные, так и нелинейные системы. Центральное место в известных методах занимает использование наблюдателей, которые могут строиться на основе различных принципов. Обычно выделяют наблюдатели состояния и выхода.

На рис. 6.4 представлен случай использования наблюдателя состояния по отношению к линейной системе:

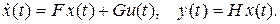
Определяющим свойством подобных наблюдателей является наличие обратной связи по невязке, а также совпадение его системных матриц с системными матрицами диагностируемой системы. В результате этих свойств система и модель могут стартовать из разных состояний, и по прошествии переходного процесса не только формируют совпадающие выходные последовательности при номинальном поведении системы и расходящиеся при наличии в системе отказов, но при этом также в 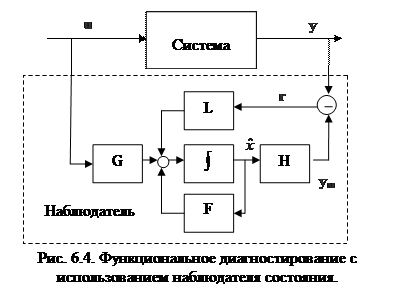наблюдателе формируется оценка состояния системы .

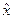Остановимся более подробно на вопросах синтеза наблюдателя состояния, поскольку далее при изложении материала будет использован именно этот тип наблюдателя. Процедура синтеза наблюдателя состояния для линейной системы известна, однако для полноты изложения приведем ее основные моменты. Для синтеза наблюдателя необходимо определить лишь матрицу обратной связи 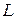. Она определяется, исходя из желаемого поведения ошибки оценивания. В соответствии со структурой на рис.6.5, если диагностируемая система и наблюдатель стартуют из разных состояний, то в наблюдателе формируется оценка вектора состояния системы. Причем поведение ошибки оценивания 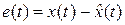определяется уравнением

.

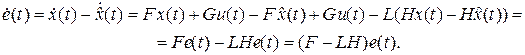Решение этого уравнения имеет вид:

,

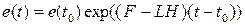где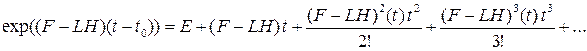

Безусловно, эта ошибка должна достаточно быстро стремиться к нулю. Для этого матрица 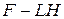должна быть устойчивой, т.е. вещественные части корней ее характеристического многочлена (собственных чисел)

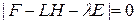
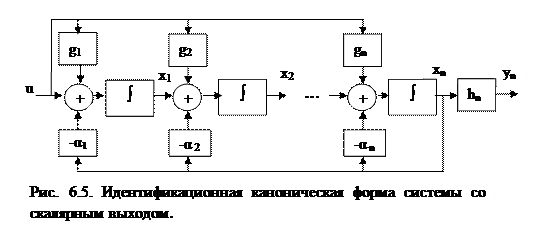
должны принимать отрицательные значения. Для случая, когда исходная система линейна, стационарна и наблюдаема алгоритм выбора матрицы 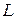известен и достаточно прост [1]. Он использует представление диагностируемой динамической системы в идентификационной канонической форме. Напомним свойства этого представления.

Сначала приведем короткую информацию об эквивалентных преобразованиях линейных динамических систем. Пусть рассматриваемая система описывается уравнениями:

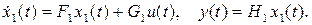
Запишем эти уравнения в другой системе координат:

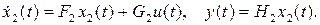
Пусть новая система координат связана с исходной неособенной матрицей преобразования T, т.е. 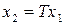. Тогда уравнения для преобразованной системы приобретают вид:

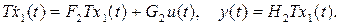
Отсюда, приравнивая выражения для выходов исходной и преобразованной систем, получаем:

.

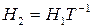Приравнивая производные от этих выходов, получаем остальные выражения:

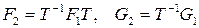
Выбирая соответствующим образом матрицу преобразования T, можно получать эквивалентные описания системы с характерными свойствами, которые называются каноническими формами. Одной из таких форм является идентификационная каноническая форма. Напомним ее свойства.

Для начала, предположим, что система имеет скалярный выход, а также для простоты и скалярный вход. Тогда она имеет структуру (рис. 6.5), в которой интеграторы вытянуты в цепочку при единственной обратной связи с выхода последнего интегратора.

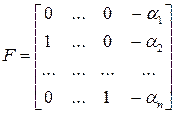
При этом, например, для номинального состояния матрицы диагностируемой системы, а, значит, и соответствующие матрицы наблюдателя имеют следующий вид.

, , , ,

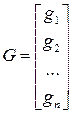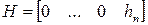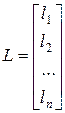где 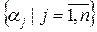– коэффициенты характеристического многочлена системы .

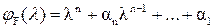При такой структуре матриц

,.

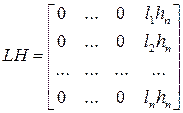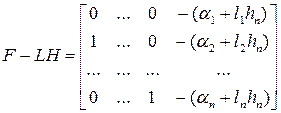Таким образом, матрица 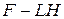имеет вид сопровождающей матрицы, где последний столбец составлен из коэффициентов характеристического многочлена . Назначив для характеристических чисел этой матрицы желаемые значения, обеспечивающие необходимую скорость стремления к нулю ошибки оценивания, можно определить коэффициенты характеристического многочлена для 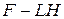, а затем и элементы матрицы обратной связи на основе соотношений .

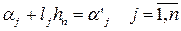В случае, когда диагностируемая система имеет много выходов, процедура определения матрицы обратной связи усложняется [1], хотя последовательность шагов остается прежней. Также, прежде всего, диагностируемую систему надо представить в идентификационной канонической форме, которая принимает более сложный вид (рис. 6.6). Она содержит уже не одну цепочку интеграторов с обратной связью с последнего интегратора, а несколько – по числу выходов системы. Эти цепочки с обратными связями на рисунке представлены прямоугольниками, обозначенными 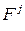. Кроме того, при упорядочивании этих компонент (цепочек) по убыванию размерности выход каждой компоненты участвует в формировании выходов всех последующих. В результате, например, для номинального состояния матрицы системы, а, значит, и соответствующие матрицы наблюдателя имеют вид:

, , ,

, , ,

.

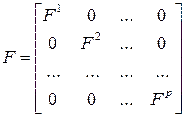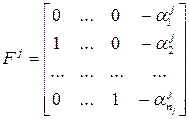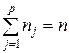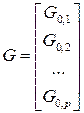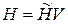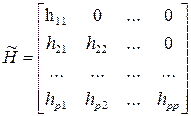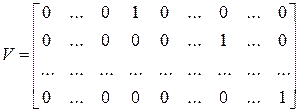В матрице V единицы стоят в столбцах с номерами 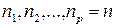. Причем 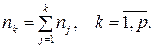Использование этой матрицы позволяет ввести в соотношения матрицу 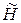, преобразующую вектор значений последних интеграторов 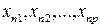в цепочках в выходной вектор 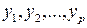системы. Для нас важно, что ввиду неособенности этой матрицы существует возможность определения вектора 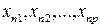по значению вектора 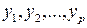. Отсюда следует, что задачу определения обратной связи в наблюдателе мы можем решать для каждой компоненты отдельно по выше изложенному алгоритму для системы с одним выходом.

Синтез наблюдателей выхода осуществляется по другим правилам. Теория построения наблюдателей выхода развита достаточно хорошо. На рис. 6.7 представлен случай, когда с помощью наблюдателя выхода диагностируется линейная система, однако известны алгоритмы построения таких наблюдателей и для нелинейных систем. В общем случае наблюдатель выхода имеет меньшую размерность, нежели диагностируемая система. В 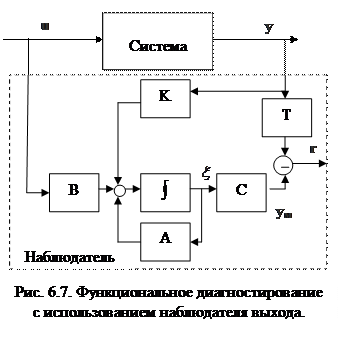связи с этим на рисунке матрицы наблюдателя имеют другие обозначения (A, B и C). Возможность получения для наблюдателя меньшей размерности связана с использованием в нем преобразователей T и K. Первый из них сужает многообразие выходных последовательностей диагностируемой системы и тем самым создает предпосылки для реализации суженного многообразия наблюдателем меньшей размерности. Второй преобразователь служит той же цели, увеличивая для наблюдателя информацию о диагностируемой системе. Необходимым условием применения этих наблюдателей и одновременно их недостатком является старт диагностируемой системы и наблюдателя из согласованных состояний. В противном случае наблюдатель будет формировать ненулевую невязку r (сигнал отказа) при номинальной работе диагностируемой системы. Случай, когда преобразователь K отсутствует, а преобразователь T реализует тождественное отображение, называют дублированием.

Диагностирование с использование наблюдателей выхода применяется не только в отношении непрерывных и дискретных, но также и цифровых систем. Последний случай активно исследовался в 70-х и 80-х годах прошлого столетия. Однако предложенные тогда методы в настоящее время в определенной степени утратили свою значимость из-за практической нецелесообразности решения задач ФД для достаточно простых устройств, которые принято описывать автоматной моделью. Тем не менее, для полноты картины коротко опишем и этот подход.

Существенную роль в этом подходе [17] играет использование результатов теории помехоустойчивого кодирования двоичной информации в каналах связи. При этом под кодом понимается набор двоичных кодовых слов, которыми представляется передаваемая по каналу связи информация. При этом каждое передаваемое слово размерности n, кроме k информационных разрядов, содержит n – k дополнительных (контрольных), которые связаны с информационными некоторыми (обычно линейными) контрольными соотношениями. При передаче через канал обмена какие-то разряды слова могут искажаться под воздействием помех. Предполагается, что в результате должны нарушаться использованные при формировании кода контрольные соотношения, поэтому, проверяя их при приеме, можно обнаружить или даже исправить возникшие искажения. Определение правил выбора контрольных соотношений и составляет содержание теории помехоустойчивого кодирования. На рис. 6.8 приведен пример кодирования исходного безызбыточного кода, содержащего восемь кодовых слов, представляющих некоторую, например, текстовую информацию. Искажение даже одного бита в любом кодовом слове будет превращать это слово в другое также разрешенное слово, а, следовательно, оно будет незамеченным. Иначе обстоит дело в избыточном коде, приведенном на том же рисунке и полученном из предыдущего кода добавлением одного разряда. Причем значение дополнительного разряда дополняет число единиц исходного слова до четного. Формально в этом случае функция кодирования (контрольное соотношение) может быть записана следующим образом: