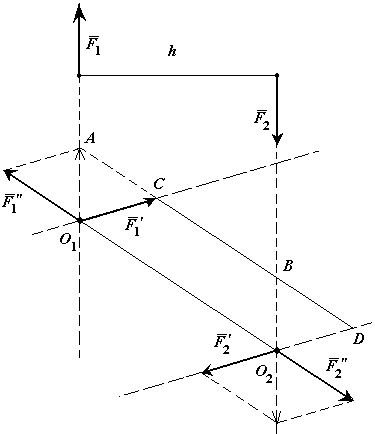
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.
Плоскостью действия пары сил называется плоскость в которой расположены эти силы.
Плечом пары сил d называется кратчайшее расстояние между линиями действия сил пары.
Моментом пары сил называется вектор 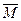 , модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия сил пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.
, модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия сил пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки. 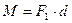
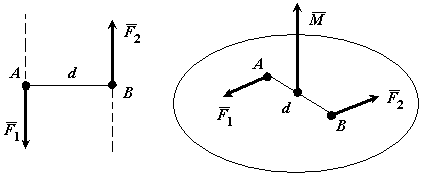 |
Рис. 4.1
Теорема о сумме моментов пары сил. Сумма моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора этой точки и равна моменту этой пары сил.
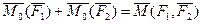
Доказательство: Выберем произвольно точку О. Проведем из нее в точки А и В радиус-векторы (Смотри Рис. 4.2).
 ,
, 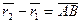
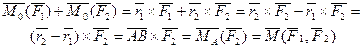
Что и требовалось доказать.
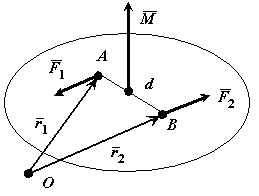 |
Рис. 4.2
Две пары сил называются эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.
Теорема об эквивалентности пар сил. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющий одинаковый с первой парой момент.
Доказательство: Пусть на твердое тело действует пара сил 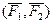 .
.
 Перенесем силу
Перенесем силу 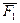 в точку
в точку 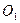 , а силу
, а силу 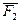 в точку
в точку 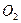 . Проведем через точки
. Проведем через точки 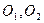 две любые параллельные прямые, пересекающие линии действия сил пары. Соединим точки
две любые параллельные прямые, пересекающие линии действия сил пары. Соединим точки 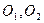 отрезком прямой и разложим силы
отрезком прямой и разложим силы 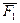 в точке
в точке 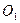 и
и 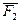 в точке
в точке 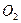 по правилу параллелограмма.
по правилу параллелограмма.
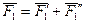
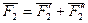
Так как 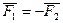 , то
, то
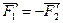 и
и 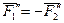
Поэтому 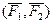 эквивалентна системе
эквивалентна системе 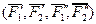 , а эта система эквивалентна системе
, а эта система эквивалентна системе 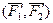 , так как
, так как 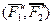 эквивалентна нулю.
эквивалентна нулю.
Таким образом мы заданную пару сил 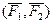 заменили другой парой сил
заменили другой парой сил 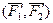 . Докажем, что моменты у этих пар сил одинаковы.
. Докажем, что моменты у этих пар сил одинаковы.
Момент исходной пары сил 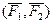 численно равен площади параллелограмма
численно равен площади параллелограмма 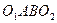 , а момент пары сил
, а момент пары сил 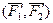 численно равен площади параллелограмма
численно равен площади параллелограмма 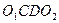 . Но площади этих параллелограммов равны, так как площадь треугольника
. Но площади этих параллелограммов равны, так как площадь треугольника 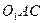 равна площади треугольника
равна площади треугольника 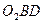 .
.
Что и требовалось доказать.
Выводы:
1. Пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия.
2. У пары сил можно изменять плечо и силы, сохраняя при этом момент пары и плоскость действия.
Теорема о переносе пары сил в параллельную плоскость. Действие пары сил на твердое тело не изменится от переноса этой пары в параллельную плоскость.
Доказательство: Пусть на твердое тело действует пара сил 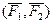 в плоскости
в плоскости 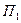 . Из точек приложения сил А и В опустим перпендикуляры на плоскость
. Из точек приложения сил А и В опустим перпендикуляры на плоскость 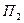 и в точках их пересечения с плоскостью
и в точках их пересечения с плоскостью 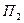 приложим две системы сил
приложим две системы сил 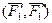 и
и 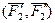 , каждая из которых эквивалентна нулю.
, каждая из которых эквивалентна нулю.
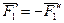
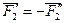
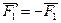
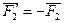
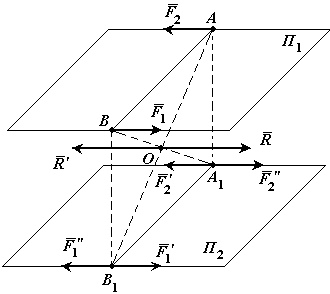 Сложим две равные и параллельные силы
Сложим две равные и параллельные силы 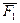 и
и 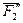 . Их равнодействующая
. Их равнодействующая 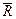 параллель-на этим силам, равна их сумме и приложена посредине отрезка
параллель-на этим силам, равна их сумме и приложена посредине отрезка 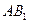 в точке О.
в точке О.
Сложим две равные и параллельные силы 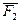 и
и 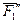 . Их равнодействующая
. Их равнодействующая 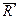 параллель-на этим силам, равна их сумме и приложена посредине отрезка
параллель-на этим силам, равна их сумме и приложена посредине отрезка 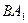 в точке О.
в точке О.
Так как 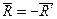 , то система сил
, то система сил 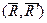 эквивалентна нулю и ее можно отбросить.
эквивалентна нулю и ее можно отбросить.
Таким образом пара сил 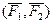 эквивалентна паре сил
эквивалентна паре сил 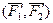 , но лежит в другой, параллельной плоскости. Что и требовалось доказать.
, но лежит в другой, параллельной плоскости. Что и требовалось доказать.
Следствие: Момент пары сил, действующий на твердое тело, есть свободный вектор.
Две пары сил, действующих на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению моменты.
Теорема о сложении пар сил. Две пары сил, действующих на одно и то же твердое тело, и лежащие в пересекающихся плоскостях, можно заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил. 
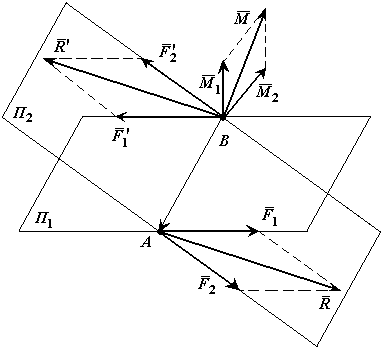 |
Доказательство: Пусть имеются две пары сил, расположенные в пересекающихся плоскостях. Пара сил 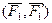 в плоскости
в плоскости 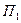 характеризуется моментом
характеризуется моментом 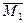 , а пара сил
, а пара сил 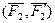 в плоскости
в плоскости 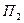 характеризуется моментом
характеризуется моментом 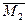 .
.
Расположим пары сил так, чтобы плечо пар было общим и располагалось на линии пересечения плоскостей. Складываем силы, приложенные в точке А и в точке В, 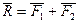
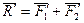 . Получаем пару сил
. Получаем пару сил 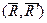 .
.
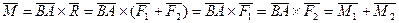
Что и требовалось доказать.
 2014-02-17
2014-02-17 8094
8094








