Выберем произвольную точку М твердого тела (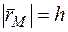 ), вращающегося вокруг неподвижной оси OZ (рис. 5). Движение точки М можно описать радиусом-вектором
), вращающегося вокруг неподвижной оси OZ (рис. 5). Движение точки М можно описать радиусом-вектором 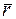 , который имеет постоянный модуль для выбранной точки:
, который имеет постоянный модуль для выбранной точки:
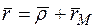 .
.
Дифференцируя (5) по времени, находим скорость:
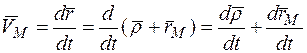 ,
,
где 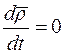 , так как вектор
, так как вектор 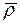 постоянен по величине и направлению как производная вектора постоянного модуля по скалярному аргументу.
постоянен по величине и направлению как производная вектора постоянного модуля по скалярному аргументу.
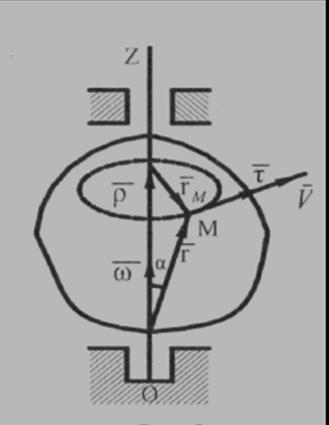
Рис.5
Тогда
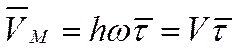
где
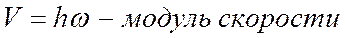 .
.
(h — расстояние от точки до оси вращения).
Вектор скорости будет направлен по касательной к траектории точки М в соответствии с направлением угловой скорости.
Задача 1. Точка А, лежащая на ободе диска, имеет скорость 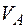 = 40 см/с. Точка В, принадлежащая диску, имеет скорость
= 40 см/с. Точка В, принадлежащая диску, имеет скорость 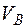 =10 см/с (рис. 6). Определить угловую скорость диска и его радиус, если расстояние АВ =15 см.
=10 см/с (рис. 6). Определить угловую скорость диска и его радиус, если расстояние АВ =15 см.
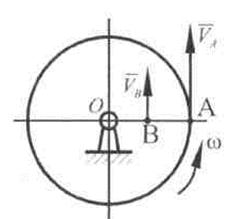
Рис. 6
Решение.
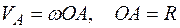 ,
,
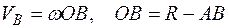 .
.
Тогда
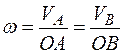 ,
,
пли
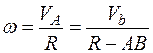 ,
,
откуда
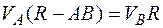 ,
,
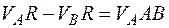 ,
,
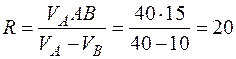 см,
см,
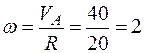 рад/с.
рад/с.
Получим векторную формулу Эйлера для скорости любой точки твердого тела, вращающегося вокруг неподвижной оси. Из рис. 5 видно, что 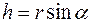 . Тогда
. Тогда 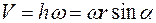 . Это выражение является модулем векторного произведения
. Это выражение является модулем векторного произведения 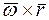 , т.е.
, т.е. 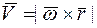 . Направление вектора скорости
. Направление вектора скорости 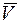 определяется векторным произведением. Следовательно:
определяется векторным произведением. Следовательно:
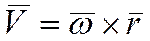 .
.
 2014-02-09
2014-02-09 669
669








