Скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости на радиус-вектор этой точки, проведенный из произвольной точки на оси вращения.
Это выражение называют векторной формулой Эйлера.
Определим ускорение точки М:
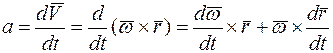 ,
,
так как
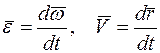 ,
,
то
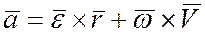 .
.
Рассмотрим слагаемые, входящие в это выражение. Вектор 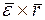 в соответствии с правилом векторного произведения направлен по касательной к траектории точки М, т. е. как касательное ускорение точки М, которое во вращательном движении называют вращательным ускорением (рис. 7):
в соответствии с правилом векторного произведения направлен по касательной к траектории точки М, т. е. как касательное ускорение точки М, которое во вращательном движении называют вращательным ускорением (рис. 7):
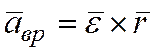 .
.
Рис. 7
Величина вращательного ускорения
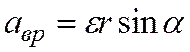 ,
,
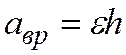 .
.
Вектор 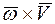 находится в плоскости окружности радиуса КМ = h, направлен от точки М к оси вращения и является нормальным ускорением точки М. При вращательном движении это ускорение называют центростремительным ускорением:
находится в плоскости окружности радиуса КМ = h, направлен от точки М к оси вращения и является нормальным ускорением точки М. При вращательном движении это ускорение называют центростремительным ускорением:
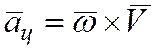 .
.
Величина центростремительного ускорения:
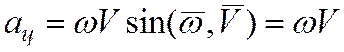 ,
,
где 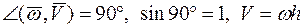 ,
,
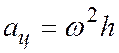 .
.
Модуль полного ускорения точки, вращающегося твердого тела
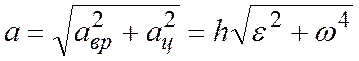 .
.
Угол между полным ускорением и центростремительным равен:
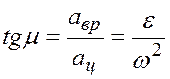 .
.
Равномерным называют вращение, при котором угловая скорость постоянна по модулю и направлению:
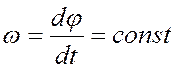 ,
,
откуда 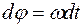 . После интегрирования получим
. После интегрирования получим
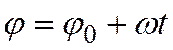 .
.
Это выражение называют законом равномерного вращения. При равномерном вращении угловую скорость можно определить, если задано число оборотов в минуту по формуле:
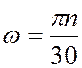 ,
,
где п — число оборотов в минуту.
Задача 2. Груз 1 опускается по закону 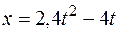 м. Определить угловую скорость, угловое ускорение барабана, скорость и ускорение точки М в момент времени t = 1 с, если R = 3 r = 0,6 м (рис. 8).
м. Определить угловую скорость, угловое ускорение барабана, скорость и ускорение точки М в момент времени t = 1 с, если R = 3 r = 0,6 м (рис. 8).
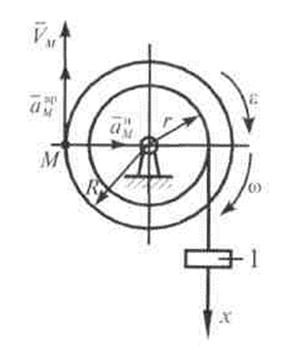
Рис. 8
Решение. Определим скорость груза:
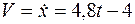 .
.
Находим угловую скорость и угловое ускорение:
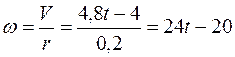 ,
,
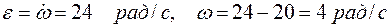 .
.
Скорость точки М равна:
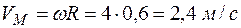 .
.
Вращательное ускорение точки М:
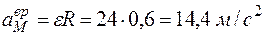 .
.
Центростремительное ускорение точки М:
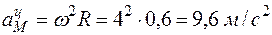 ,
,
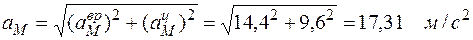
Модуль полного ускорения точки М можно найти по формуле (15):
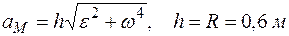 ,
,
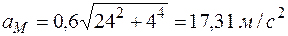 /
/
Равнопеременным называют вращение, при котором угловое ускорение постоянно по величине и направлению:
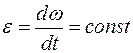 .
.
Откуда 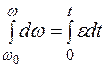 .
.
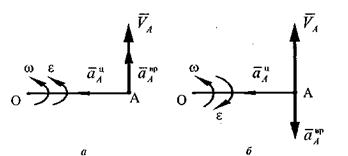
Рис. 9
Находим
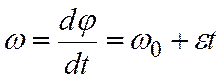 .
.
После разделения переменных и интегрирования
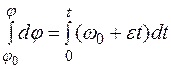
получим
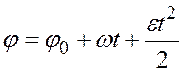
- закон равнопеременного вращения
Если ω и ε имеют одинаковые знаки, то вращение равноускоренное (рис. 9, а). Скорость и вращательное ускорение направлены в одну сторону.
Если ω и ε имеют разные знаки, то вращение равнозамедленное. Скорость и вращательное ускорение направлены в разные стороны (рис. 9, б). Центростремительное ускорение в обоих случаях направлено к оси вращения.
Задача 3. Диск, вращаясь равноускоренно из состояния покоя, сделал 14400 оборотов за 4 мин. Определить угловую скорость и угловое ускорение диска.
Решение. Начальные условия движения: 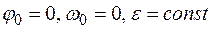 ω.
ω.
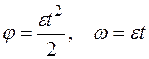 .
.
 Используя формулу
Используя формулу 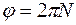 , находим угловое ускорение диска:
, находим угловое ускорение диска:
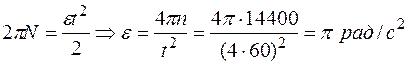 .
.
Угловая скорость равна: 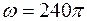 рад/с.
рад/с.
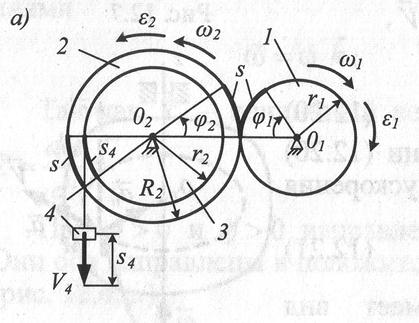
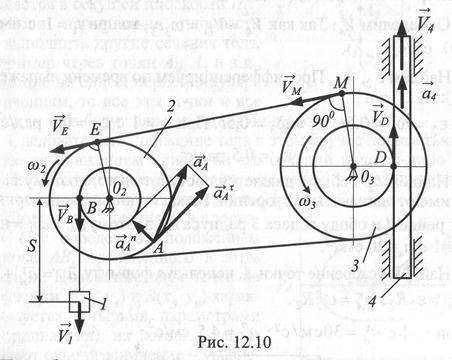
Задача 4. Для спуска груза 4 диск 1 вращается вокруг неподвижной оси, проходящей через его центр 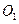 , перпендикулярно плоскости диска, согласно уравнению
, перпендикулярно плоскости диска, согласно уравнению 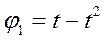 и приводит во вращение диски 2 и 3 жёстко скрепленные друг с другом и имеющие общую неподвижную ось вращения. Диски 1 и 2 являются зубчатой передачей.
и приводит во вращение диски 2 и 3 жёстко скрепленные друг с другом и имеющие общую неподвижную ось вращения. Диски 1 и 2 являются зубчатой передачей.
Определить скорость и ускорение груза 4, ускорение точки А в момент времени t=5 с, если 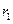 =0,2 м;
=0,2 м;  =0,4 м;
=0,4 м;  =0,3 м.
=0,3 м.
Сначала определим угловую скорость и угловое ускорение диска 1.
В момент времени t=5 с определим модуль угловой скорости
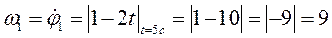 рад/с; модуль
рад/с; модуль 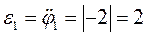 рад/
рад/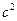 .
.
Дуговые стрелки для 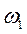 и
и 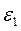 , соответствующие направлению и характеру вращения диска 1, следует направить в сторону движения часовой стрелки, т. к. алгебраические угловая скорость
, соответствующие направлению и характеру вращения диска 1, следует направить в сторону движения часовой стрелки, т. к. алгебраические угловая скорость 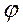 и угловое ускорение
и угловое ускорение 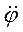 оказались отрицательными. Тогда диски 2 и З будут вращаться против движения часовой стрелки за счёт зубчатой передачи. Запишем уравнения связи. Для этого, согласно выражению свяжем перемещение точек соприкосновения диска 3 и тела 4 (через нерастяжимый трос):
оказались отрицательными. Тогда диски 2 и З будут вращаться против движения часовой стрелки за счёт зубчатой передачи. Запишем уравнения связи. Для этого, согласно выражению свяжем перемещение точек соприкосновения диска 3 и тела 4 (через нерастяжимый трос):
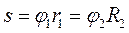 , получаем
, получаем 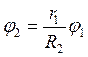 ;
; 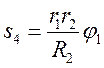 .
.
Дифференцируем правые и левые части полученного равенства:
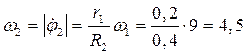 рад/с;
рад/с; 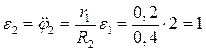 рад/
рад/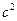 ;
;
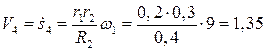 м/с;
м/с; 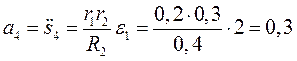 м/
м/ .
.
Вычислим уравнение точки А на диске:
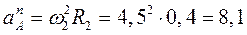 м/
м/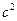 ;
; 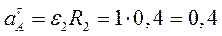 м/
м/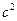 ;
;
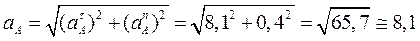 м/
м/ .
.
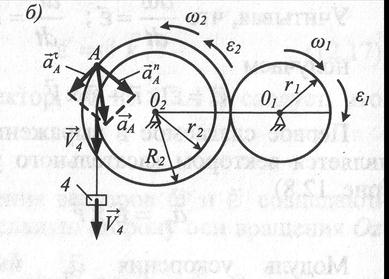
Задача 5. Груз 1(рис. 12.10), опускаясь, согласно уравнению s = 3 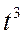 +15, где s - расстояние груза от места схода нити с поверхности вала в сантиметрах; t - время в секундах, приводит в движение колесо 2, ременную передачу, колесо 3 и рейку 4.
+15, где s - расстояние груза от места схода нити с поверхности вала в сантиметрах; t - время в секундах, приводит в движение колесо 2, ременную передачу, колесо 3 и рейку 4.
Пренебрегая скольжением ремня по ободам колес, определить для момента времени 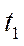 =1 с скорость и ускорение рейки 4, угловые скорости и ускорения колёс 2, 3 и ускорение точки А, если
=1 с скорость и ускорение рейки 4, угловые скорости и ускорения колёс 2, 3 и ускорение точки А, если 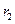 =30 см;
=30 см; 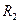 =50 см - радиусы ступеней колеса 2;
=50 см - радиусы ступеней колеса 2; 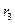 =40 см;
=40 см; 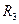 =60 см - радиусы ступеней колеса 3.
=60 см - радиусы ступеней колеса 3.
Дано: 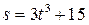 ;
;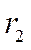 =30 см;
=30 см;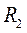 =50 см;
=50 см; 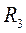 =60 см.
=60 см.
Определить:  при
при 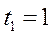 с.
с.
1. Найдём 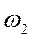 ,
, 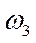 . Зная уравнение движения груза 1, определим его скорость как функцию времени
. Зная уравнение движения груза 1, определим его скорость как функцию времени 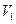 =
=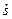 = 9
= 9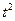 . Груз подвешен на нерастяжимом канате, поэтому скорость груза 1 такая же, как скорости точек на ободе колеса 2 радиуса
. Груз подвешен на нерастяжимом канате, поэтому скорость груза 1 такая же, как скорости точек на ободе колеса 2 радиуса 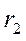 , т.е.
, т.е. 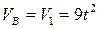 . Найдем
. Найдем 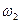 как функцию времени:
как функцию времени:
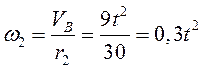 . (а)
. (а)
Так как колёса 2 и 3 связаны ременной передачей (ремень нерастяжим), то 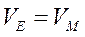 , но
, но 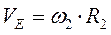 ;
; 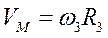 .
.
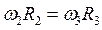 ,
,
поэтому
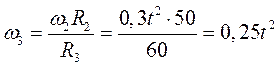 . (б)
. (б)
При t=1 с из (а) и (б) найдем = 0,3 рад/с; =-,25 рад/c.
2. Определим 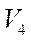 . Так как
. Так как 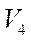 =
=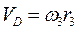 , то при
, то при 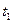 =1 с имеем
=1 с имеем 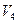 =10 см/c.
=10 см/c.
3. Найдем 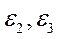 . Продифференцируем по времени выражения (а), (б):
. Продифференцируем по времени выражения (а), (б):
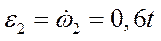 ;
; 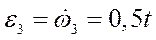 . При
. При 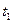 =1с
=1с 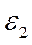 =0,5 рад/
=0,5 рад/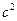 .
.
4. Найдем 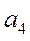 . Рейка 4 движется поступательно, поэтому все её точки имеют одинаковые ускорения. Точка D одновременно принадлежит рейке 4 и ободу колеса 3 радиуса
. Рейка 4 движется поступательно, поэтому все её точки имеют одинаковые ускорения. Точка D одновременно принадлежит рейке 4 и ободу колеса 3 радиуса 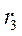 , поэтому
, поэтому 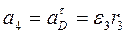 ; при
; при 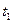 =1с и
=1с и 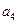 =20 см/
=20 см/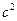
5. Найдем ускорение точки А, используя формулу 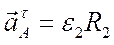 ;
;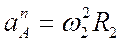 .
.
При 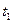 =1с и
=1с и 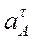 =30 см/
=30 см/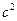 ;
; 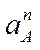 =4,5 см/
=4,5 см/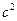 ;
;
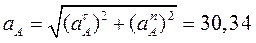 см/
см/ .
.
 2014-02-09
2014-02-09 12211
12211