Построение эпюр

Диаграммы изменения нормальной силы, напряжений и перемещений стержня вдоль его оси называются эпюрами соответственно продольных (нормальных) сил, напряжений и перемещений.

Рассмотрим пример построения таких эпюр для стержня, изображенного нна рис.2.3. Начало координат О принято в неподвижном сечении (в заделке), а ось координат z совпадает с осью стержня и направлена вниз.

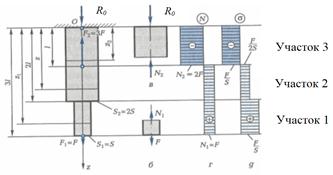
Рис.2.3. Стержень под действием осевых

нагрузок и эпюры продольных (нормальных)

сил и напряжений при площади поперечного

сечения стержня на участках А₁ = S, A_2,3 = 2S

Из уравнения равновесия стержня определяем силу R ₀ реакции связи в заделке

S Z = 0: R ₀ – 3 F + F = 0, откуда найдем R ₀ = 2 F.

При построении эпюр используется метод сечений по участкам, различаемым по размерам поперечных сечений и внешним силовым факторам. В рассматриваемой задаче таких участков три (рис.2.3, а): 1 – от свободного конца стержня до перепада поперечного сечения на больший размер (на интервале расстояний 2 l … 3 l); 2 – от первого участка до места приложения силы 3F (на интервале расстояний l … 2 l от заделки); 3 - от заделки до места приложения силы 3F (на интервале 0 … l);

Для построения эпюры внутренних продольных сил N на первом участке запишем уравнение силового равновесия для любой отсеченной его части на расстоянии z ₁ (рис.2.3, б):

S Z = 0: - N ₁ + F = 0, откуда находим N ₁ = F.

Аналогично найдем для второго участка N ₂ = F и для третьего участка N ₃ = 2 F. По результатам этих расчетов построена эпюра продольных сил (рис.2.3, г).

С учетом эпюры продольной силы строится эпюра нормальных напряжений в поперечных сечениях на участках 1-3 (рис.2.3, д) в соответствии с уравнением 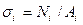, где А _i – площадь поперечного сечения стержня на i -м участке.