Эллипс
Линии 2-го порядка
1. Возьмем на плоскости две точки 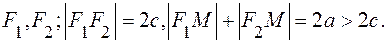
Опр. Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами,
есть величина постоянная, большая расстояния между фокусами.
2. Составим уравнение эллипса.
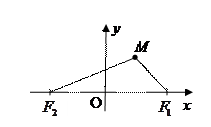 Выберем систему координат
Выберем систему координат 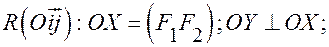
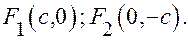 Пусть точка
Пусть точка 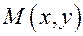
принадлежит эллипсу 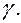
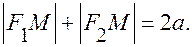
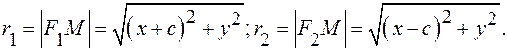
 |
 (3)
(3)
Преобразуем уравнение (1), возводя в квадрат обе части:
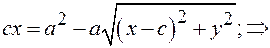
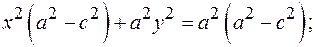
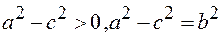
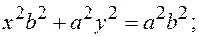
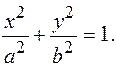 (4)
(4)
Мы показали, что координаты точек эллипса удовлетворяют уравнению (4). Но при переходе от (3) к (4) мы дважды возводили уравнение в квадрат, при этом могли появиться лишние корни. Убедимся, что точки, координаты которых удовлетворяют уравнению (4), принадлежат эллипсу, то есть 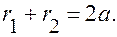
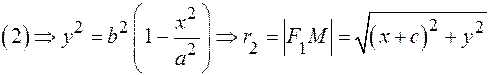 =
=
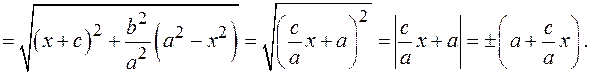 Аналогично:
Аналогично: 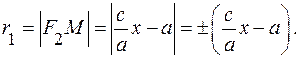
Так как 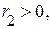 то
то 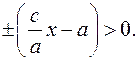 Из (2)
Из (2) 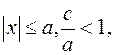 поэтому
поэтому
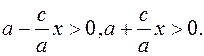 Значит,
Значит,
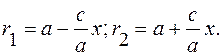 (5)
(5)
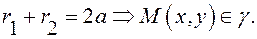
Уравнение (4) называется каноническим уравнением эллипса.
Формулы (3) дают фокальные радиусы эллипса
3. Исследование формы эллипса.
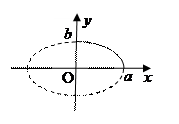 Если
Если 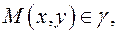 то
то 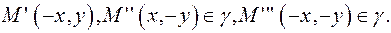 То есть у эллипса есть две оси симметрии
То есть у эллипса есть две оси симметрии 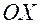 и
и 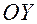 центр симметрии
центр симметрии 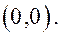 Точки пересечения эллипса с осями координат называются его вершинами. Пользуясь симметрией эллипса, рассмотрим его форму в 1 четверти.
Точки пересечения эллипса с осями координат называются его вершинами. Пользуясь симметрией эллипса, рассмотрим его форму в 1 четверти.
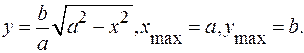
При росте 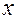 от 0 до
от 0 до 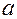
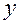 убывает от
убывает от 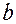 до 0.
до 0.
Продолжим чертеж симметрично в другие четверти.
Как видно, эллипс – линия ограниченная, расположенная в прямоугольнике 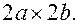 Вершины
Вершины 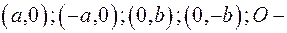 центр эллипса.
центр эллипса.
Заметим, что фокусы эллипса всегда принадлежат большей оси.
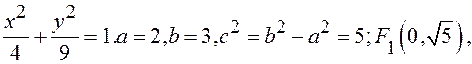
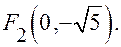
4. Эксцентриситет эллипса.
Опр.Эксцентриситет 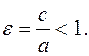
При 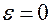 фокусы совпадают:
фокусы совпадают: 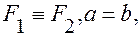 эллипс является окружностью. Найдем:
эллипс является окружностью. Найдем: 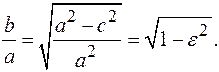
Как видно, чем меньше 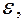 тем дробь
тем дробь 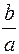 ближе к 1, то есть эллипс становится шире. Чем больше
ближе к 1, то есть эллипс становится шире. Чем больше 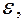 тем больше эллипс вытянут вдоль оси
тем больше эллипс вытянут вдоль оси 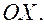
5. Параметрические уравнения эллипса.
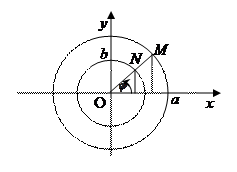 Пусть задан эллипс
Пусть задан эллипс
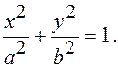 Построим две
Построим две
окружности 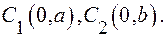
Произвольный луч под углом 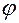 к оси
к оси 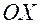
пересекает их в точках 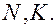 Построим точку
Построим точку 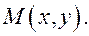 Очевидны равенства:
Очевидны равенства:
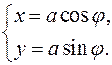 (6)
(6)
Подставив (6)в уравнение эллипса, получим верное равенство, следовательно, точка 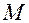 принадлежит эллипсу. Уравнения (6) называются параметрическими уравнениями эллипса.
принадлежит эллипсу. Уравнения (6) называются параметрическими уравнениями эллипса.
Замечание. Можно доказать обратное утверждение: если точка принадлежит эллипсу, то найдется значение параметра 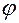 такое, что выполняются соотношения (6).
такое, что выполняются соотношения (6).
Отсюда ясен способ построения эллипса.
6. Директрисы эллипса.
 Опр. Директрисами эллипса называются прямые, параллельные малой оси и отстоящие от неё на расстояние
Опр. Директрисами эллипса называются прямые, параллельные малой оси и отстоящие от неё на расстояние 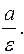
Очевидны уравнения директрис:
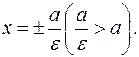
Найдем отношение расстояний точки 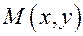 эллипса до фокуса и до соответствующей директрисы. Расстояния до фокусов дают формулы (5):
эллипса до фокуса и до соответствующей директрисы. Расстояния до фокусов дают формулы (5):
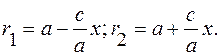
Расстояния до директрис: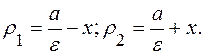 Отсюда:
Отсюда:
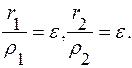
Свойство директрис эллипса: эллипс есть множество точек, отношение расстояний от каждой из которых до фокуса к расстоянию до соответствующей директрисы постоянно и равно эксцентриситету.
Задача. Составьте уравнение эллипса, если расстояние между директрисами 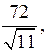 а между фокусами
а между фокусами 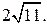
 2014-02-09
2014-02-09 823
823








