Взаимное расположение двух прямых

7.3.1. Выясним, при каких условиях два уравнения

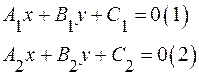
определяют одну и ту же прямую?

Теорема 10. Для того, чтобы уравнения (1) и (2) определяли одну и ту же прямую, необходимо и достаточно, чтобы их коэффициенты были пропорциональны.

∆ Пусть (1) и (2) определяют одну и ту же прямую.

Необходимость 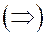Направляющие векторы этих прямых:

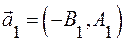и 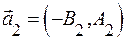коллинеарны, следовательно,

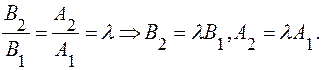
Возьмем на прямой точку 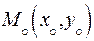, подставим её координаты в уравнения (1) и (2) и вычтем, умножив (1) на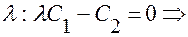

√

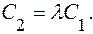ДостаточностьЕсли коэффициенты уравнений (1) и (2) пропорциональны, то (2) можно записать так:

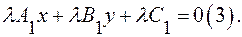Но уравнениям (2) и (3) удовлетворяют координаты одних и тех же точек, следовательно, они определяют одну и ту же прямую. ▲

7.3.2. Выясним взаимное расположение двух прямых, заданных в некоторой аффинной системе координат уравнениями (1) и (2).Возможны два случая.

1.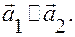В этом случае прямые пересекаются, и для нахождения их точки пересечения надо решить систему уравнений (1),(2).

2.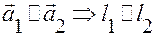ил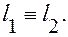и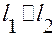

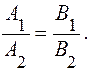При При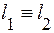

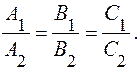
Вывод. 1)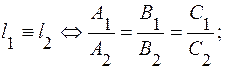

2)

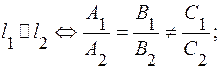
3)

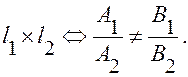
Задача. Через точку 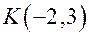провести прямую, параллельную прямой

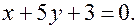Решить двумя способами.