8.1. Рассмотрим на плоскости две аффинные системы координат:
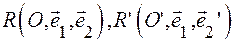 (старая и новая системы координат).
(старая и новая системы координат).
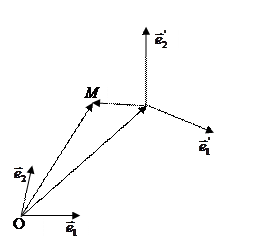 Пусть точка
Пусть точка 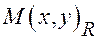 и
и 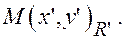
Задача преобразования координат состоит в
следующем: выразить старые координаты
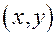 точки через новые
точки через новые 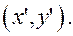
Зададим систему 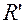 относительно
относительно 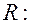
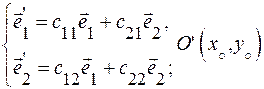 (1)
(1)
По правилу треугольника получим: 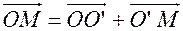 или
или 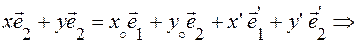 (используем (1))
(используем (1))
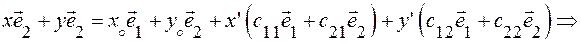
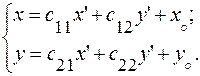 (2)
(2)
Формулы (2) называются ф ормулами преобразования координат. 
Заметим, что матрица 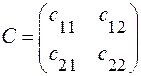 перехода от базиса
перехода от базиса 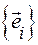 к базису
к базису 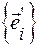 в точности совпадает с матрицей из коэффициентов при
в точности совпадает с матрицей из коэффициентов при
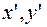 в формулах (2). Определитель этой матрицы
в формулах (2). Определитель этой матрицы 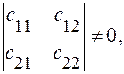 поэтому система (2) разрешима относительно
поэтому система (2) разрешима относительно 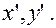
Интересны два частных случая.
(А) Перенос начала.
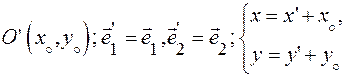
(В) Замена координатных векторов.
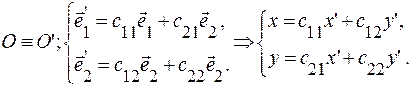
Пример. Написать формулы преобразования координат в аффинной системе, если
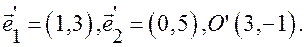
∆ 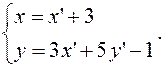 ▲
▲
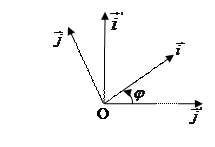
8.2. Рассмотрим преобразование прямоугольных координат. Дпск есть частный случай аффинной системы, поэтому можно использовать формулы (2). На коэффициенты матрицы перехода С накладываются определенные условия.
Возможны два случая.
С) Системы 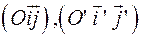 ориентированы одинаково (обе правые).
ориентированы одинаково (обе правые).
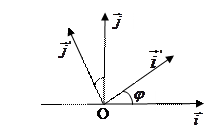
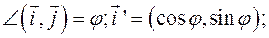
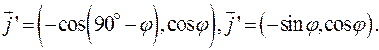
Формулы (2) запишутся так:
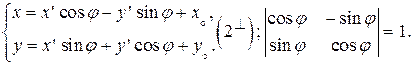
D) Системы 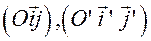 ориентированы противоположно.
ориентированы противоположно.
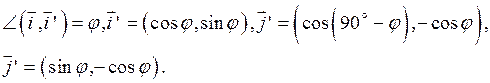
Формулы (2) запишутся так:
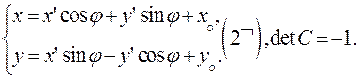
Объединим Формулы 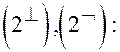
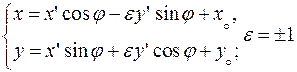 . (3)
. (3)
(«+» для одинаково ориентированных систем).
Задача. Определите координаты новых векторов и нового начала, если формулы преобразования имеют вид:
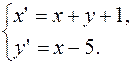 отв.
отв.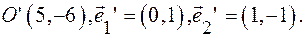
Задача. Напишите формулы преобразования прямоугольных декартовых координат, если 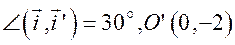 и системы
и системы 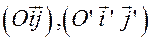 одинаково ориентированы.
одинаково ориентированы.
Отв. 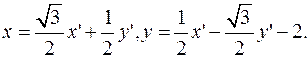
 2014-02-09
2014-02-09 6496
6496
