Решение системы связанных ИУ

Система связанных ИУ для двухэлементной вибраторной антенной решетки с активным питанием (вывод).

Частотная зависимость входного сопротивления симметричного вибратора.

На основе выражения (8.4.15) можно получить частотную зависимость входного сопротивления симметричного вибратора (рис.8.5.1.). Отметим здесь несколько характерных точек:

9.Математическое описание вибраторных антенных решеток.

Интегральное уравнение Поклингтона, выведенное в предыдущем разделе ниже обобщается на вибраторные антенные решетки - антенны волновой канал, фазированные антенные решетки и.т.д. В этом случае математическое описание сводится к системе связанных интегральных уравнений такого порядка, каково число излучателей. Для проектирования антенных решеток наличие точной математической модели совершенно необходимо, поскольку в этом случае число степеней свободы (длины вибраторов, расстояние между ними) гораздо больше, чем в случае одиночного вибратора.

Для повышения направленности простейшие вибраторные излучатели объединяют в упорядочные структуры - антенные решетки (рис.9.1.).

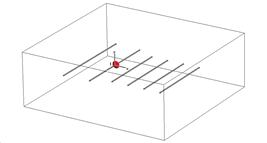
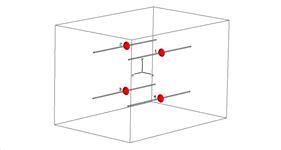
а) б)

Рис. 9.1

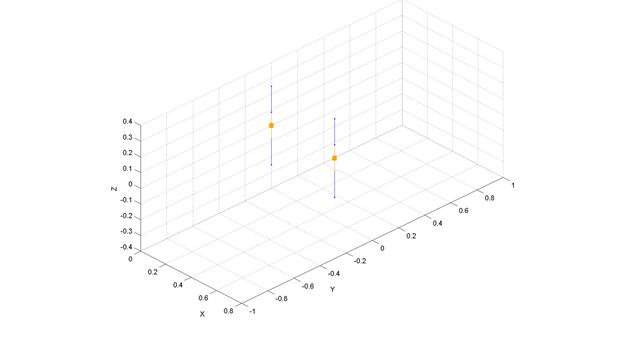
Рис.9.1. в)

Запишем теорему запаздывающих потенциалов для антенной решетки, состоящей из двух параллельных вибраторов одинаковой длины и радиуса, расположенных на расстоянии друг от друга (рис.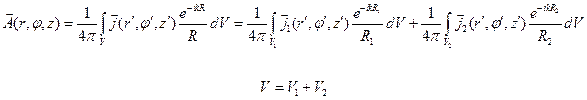9.1.):

(9.1)

Объем 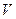, занятый токами в данном случае распадается на две несвязанные области:- объем первого 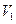и второго вибратора 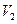, причем в выражении 9.1. под знаком первого интеграла стоит вектор плотности тока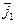, а под знаком второго - 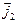, 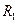и 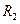- расстояния между точкой интегрирования в пределах первого и второго объемов соответственно и произвольной точкой наблюдения с координатами .

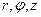В случае большего числа элементов в решетке выражение 9.1. немного усложнится- число интегралов будет равно числу элементов.

Основываясь на тех же допущениях, что и при выводе уравнения Поклингтона одиночного вибратора (т.е. наличие сильного скин-эффекта, приближение тонкого провода) векторный потенциал на поверхности первого и второго вибратора можно привести к виду:

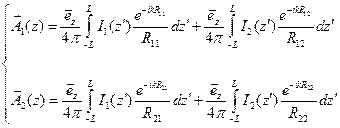(9.2)

где: 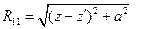- расстояние между текущей точкой наблюдения на оси и точкой на поверхности первого вибратора, очевидно, что такое же расстояние будет и для второго вибратора, т.е. ,

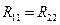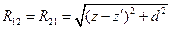- расстояние между точкой интегрирования на оси первого и точкой наблюдения на поверхности второго вибратора. От системы уравнений (9.2) для векторного потенциала легко перейти к аналогичной системе для вектора напряженности электрического поля:

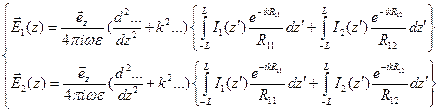. (9.3.)

В точном соответствии с той же последовательностью действий, что и при выводе уравнения Поклингтона одиночного вибратора теперь следует записать пару граничных условий относительно касательной компоненты электрического поля на поверхности первого и второго вибраторов:

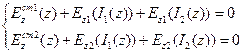(9.4.)

В этой записи 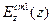,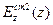- стороннее электрическое поле, создаваемое источниками, возбуждающими первый и второй вибраторы соответственно, 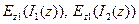- касательная компонента электрического поля на поверхности первого вибратора, обусловленная токами в первом и втором вибраторах, а 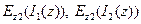- касательные компоненты на поверхности второго вибратора, обусловленная теми же токами. Из системы 9.4 вытекает окончательная системы связанных интегральных уравнений типа Поклингтона относительно токов в первом и втором вибраторах:

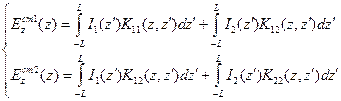, (9.5.)

где ядра системы:

,

,

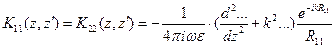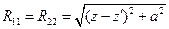
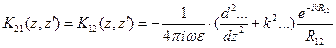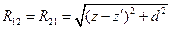
Полученная система (9.5) описывает в самосогласованной постановке систему из двух вибраторов с учетом взаимного влияния их друг на друга, в частном случае, при отсутствии взаимной связи (например, в случае значительного междуэлементного расстояния, т.е. при 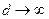) ядра 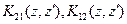стремятся к нулю. Легко убедиться, что в этом случае система (9.5) распадается на две независимые системы относительно тока в первом и во втором вибраторе соответственно (т.е. на два независимых уравнения Поклингтона).

Система (9.5) решается аналогично:

1 Этап. Выбираем систему базисных функций 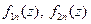, по которым раскладывается предполагаемое решение на первом и втором вибраторах:

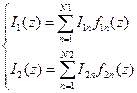(9.6)

Здесь возможна ситуация, в которой число базисных функций на первом и втором вибраторе неодинаково: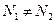, а их вид на разных вибраторах разный.

2 Этап. Подставляем разложение (9.6) в исходную систему интегральных уравнений (8.3.3) и меняя порядок суммирования и интегрирования, получаем:

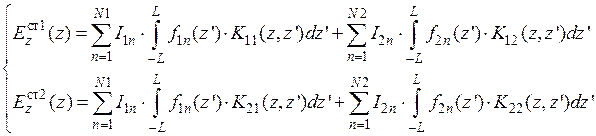(9.7)

3 Этап. Формирование системы линейных алгебраических уравнений также выполним методом Галеркина. На этом этапе конкретизируем и упростим ситуацию, будем считать, что ток на каждом вибраторе описывается тремя одинаковым базисными функциями: 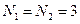, 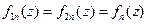. Далее, последовательно умножая правую и левую части уравнений системы 9.7 на проекционные функции 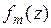, получим СЛАУ шестого порядка относительно неизвестных базисных коэффициентов на каждом вибраторе:

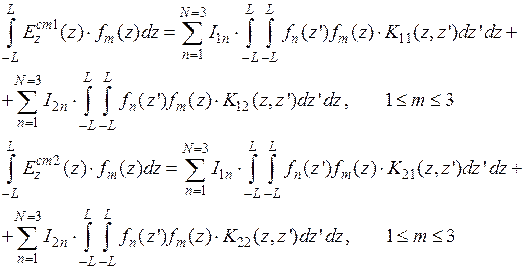(9.8)

Эту систему можно переписать в другом виде, введя сквозную нумерацию базисных функций и токов:

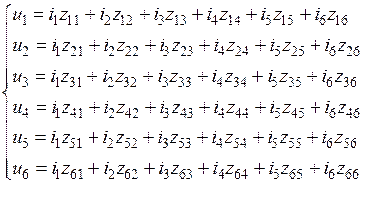(9.9)

Здесь 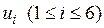- амплитуды напряжения, выражаемые через интегралы от напряженности стороннего электрического поля, причем вектор–столбец левых частей выглядит т.о:

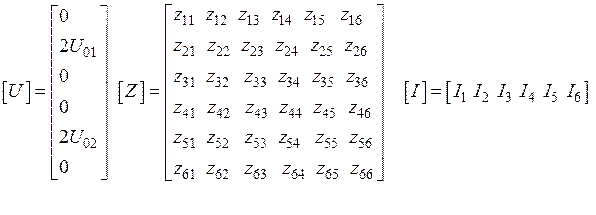где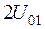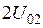- напряжения дельта-источников напряжения, включенных в центре каждого вибратора. Остальные элементы вектора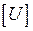равны нулю. В матрице обобщенных взаимных импедансов 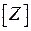диагональные блоки (верхний левый и правый нижний блоки):

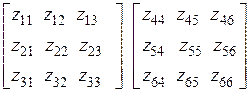
отвечают за взаимодействие сегментов в пределах первого и второго вибраторов соответственно. Внедиагональные блоки (правый верхний и левый нижний) описывают взаимное влияние сегментов, между первым и вторым вибраторами:

.

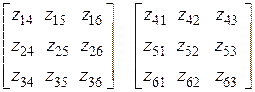4 Этап. На этом этапе надо решить систему уравнений (9.9), причем в данном случае целесообразно использовать специальные алгоритмы для решения системы с так называемой блочно-теплицевой матрицей. В результате решения будут найдены амплитуды токов (система базисных коэффициентов).

5 Этап. Восстанавливаются по найденным коэффициентам распределения токов в каждом вибраторе, затем находятся входные сопротивления каждого вибратора и ДН всей системы.

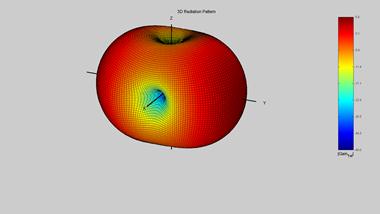
Рис.9.10 ДН при синфазном возбуждении двух вибраторов,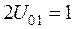

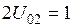
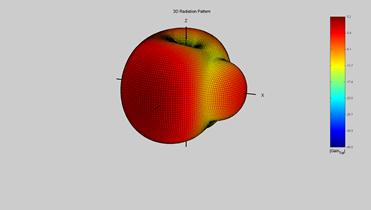
Рис.9.11. ДН системы из двух активных вибраторов при ,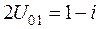

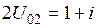
Рис. 9.12. ДН системы из двух активных вибраторов при ,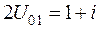

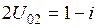
Результаты решения системы и вычисления ДН решетки из двух активных вибраторов представлены на рис. 9.10-9.12. Форма ДН существенно зависит от соотношения фаз генераторов. При синфазном возбуждении форма ДН мало меняется в азимутальной плоскости, за исключением некоторого узкого интервала частот. ДН представлена на рис.9.10. При сдвиге фаз между генераторами 90 град ДН приобретает выраженную направленность, таким образом можно реализовать управление положением главного лепестка ДН электронным образом в вибраторных малоэлементных антенных решетках. Гораздо проще реализовать направленное излучение в антеннах «волновой канал», в которых возбуждается только один элемент, а остальные (пассивные) возбуждаются через электромагнитную связь, причем фаза и амплитуда в них существенно зависит от геометрии их взаимного расположения.

9.3.Система связанных интегральных уравнений для многоэлементной антенны «волновой канал».

Вибраторная антенная решетка с продольным излучением (ВК) для своего математического описания требует системы связанных интегральных уравнений такого порядка, сколько элементов, например для шестиэлементной антенны, представленной на рис. 9.1. искомыми являются семь функций распределения токов в рефлекторе, активном элементе и четырех директорах. Некоторое отличие от описанной ранее системы, помимо чисто количественных заключается в неравенстве длин элементов. В этом случае, проводя те же рассуждения, можно записать систему связанных интегральных уравнений:

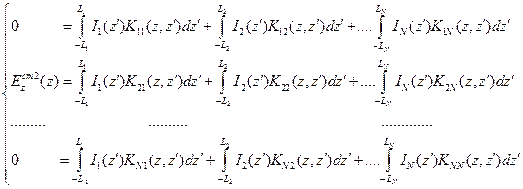, (9.10.)

Нулевые значения стороннего электрического поля во всех строчках системы (9.10) кроме второй объясняются отсутствием возбуждающего источника во всех элементах кроме активного (второго). Физический смысл системы интегральных уравнений (9.10) заключается в том, что каждая строчка – это запись граничного условия для касательной компоненты электрического поля на поверхности каждого вибратора, причем каждый интеграл в правой части любой строки системы (9.10) - это вклад в поле на поверхности одного из вибраторов от каждого из 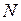элементов антенной решетки, таким образом, общее число интегралов в системе равно квадрату числа элементов решетки.

Ядра системы (9.10) содержат в себе информацию о взаимном расположении элементов, при одинаковой толщине каждого вибратора:

,

,

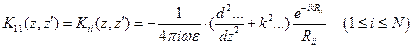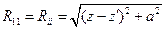
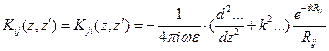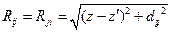
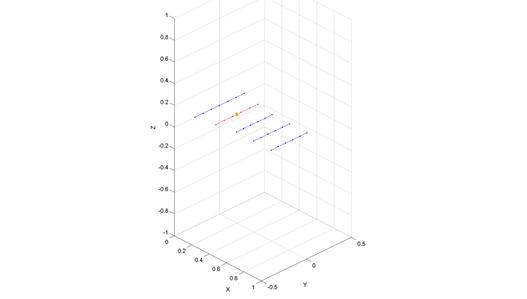
Рис.9.13. Геометрия 5-элементной решетки «волновой канал»

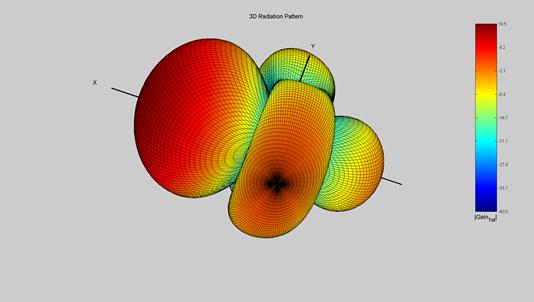
Рис.9.14. 3-Д диаграмма направленности 5-элементной антенной решетки «волновой канал»

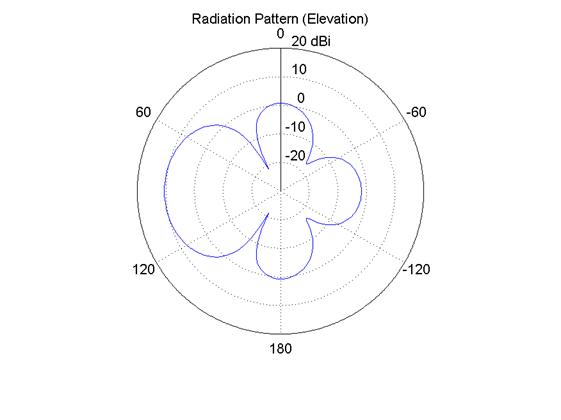
Рис.9.15. 2-Д диаграмма направленности 5-эл. решетки «волновой канал»

Решение системы интегральных уравнений (9.10) выполняется тем же способом, что для системы (9.5), небольшое непринципиальное отличие заключается только в общем числе неизвестных функций и в числе соответствующих базисных коэффициентов, что приводит в свою очередь к увеличению размерности системы линейных алгебраических уравнений.