2014-02-09
2486
Распределение тока, найденное из аналогии между антенной (принципиально диссипативная система) и длинной линией без потерь (формула 8.2) не дает возможности определить входное сопротивление вибратора с достаточной точностью в широкой полосе частот. Для этого следует использовать более точную математическую модель, основанную на самосогласованной постановке. Такая постановка приводит к формулировке интегродифференциального уравнения относительно распределения тока.
Основываясь на связи векторного потенциала и распределения тока в тонком идеально проводящем цилиндрическом вибраторе, возбуждаемом в центре идеальным источником напряжения и переходя от векторного потенциала к вектору напряженности электрического поля, удается записать граничное условие на поверхности антенны. Такая запись граничного условия и приводит к уравнению Поклингтона.
8.3.1.Векторный потенциал цилиндрического вибратора:
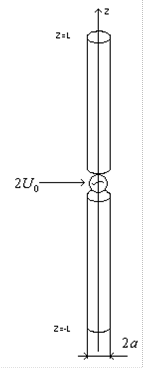
Рис. 8.3.1.
При выводе выражения для векторного потенциала будем исходить из содержания теоремы запаздывающих потенциалов и ряда приближений:
1) Антенна идеально проводящая: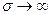 
.
2) Радиус проводника антенны много меньше ее длины.
Вычислим векторный потенциал на поверхности антенны. Исходя из теоремы запаздывающих потенциалов в цилиндрической системе координат векторный потенциал определяется как:
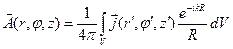
Здесь: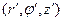 
- координаты точки интегрирования, 
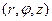- координаты точки наблюдения, 
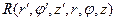– расстояние между точкой наблюдения и точкой интегрирования, V – объем занимаемый токами. Учитывая наличие сильного скин-эффекта, будем считать, что ток течет в бесконечно тонком слое по поверхности проводника (рис.8.3.2.а).
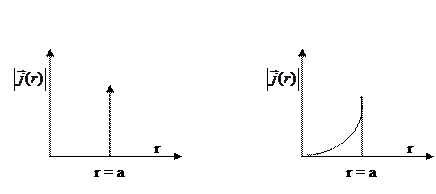
а)идеальный проводник б) реальный металл
Рис. 8.3.2.
Таким образом, математически вектор плотности тока можно записать в виде: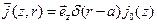 
, здесь 
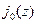- неизвестная скалярная функция. Для ее определения подставим последнее выражение в известное соотношение: 
.
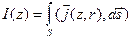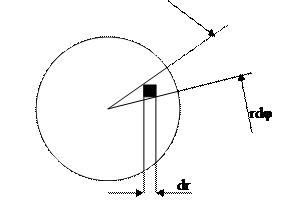
Рис. 8.3.3.
Элемент поверхности запишется так: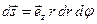 
, интеграл легко берется с учетом фильтрующего действия дельта- функции:
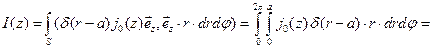
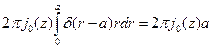
Отсюда окончательно получим: выражение для вектора плотности тока: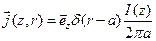 
.
Теперь можно окончательно записать векторный потенциал:
.
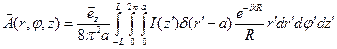Для выражения расстояния между точками наблюдения и интегрирования выделим две точки на поверхности антенны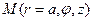 
и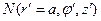 
.
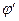
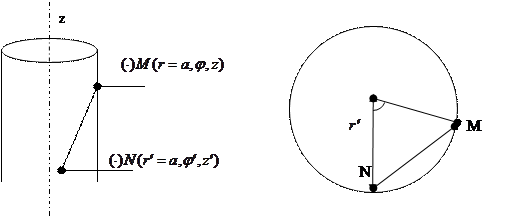
Рис. 8.3.4.
При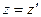 
можно воспользоваться теоремой косинусов: 
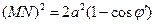. Тогда для произвольных 
мы можем записать: 
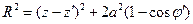. Учитывая, что радиус антенны весьма мал, можно использовать приближенное среднее значение 
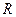, не зависящее от угла. Действительно, из рис. 8.3.4. видно, что 
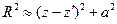, в итоге получаем:
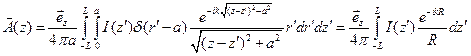. (8.3.1)
8.3.2.Электрическое поле на поверхности цилиндрической антенны.
Как известно, связь электрического поля и векторного потенциала имеет вид:
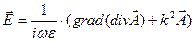. Найдем 
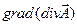учитывая, что векторный потенциал имеет только одну продольную составляющую, как это видно из выражения (8.3.1): 
:
,
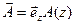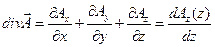Градиент этого выражения в силу зависимости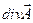 
только от координаты 
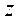будет иметь только 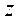-ую проекцию:
.
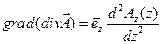Теперь найдем электрическое поле:
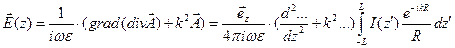. (8.3.2.)
Итак, мы получили выражение для вектора напряженности электрического поля, обусловленного током, протекающим по проводнику и зависящему от геометрии антенны, длины волны, свойств среды.
