Решение уравнения Поклингтона методом Галеркина

Аналитического решения уравнения (8.3.3.) не найдено. Численное решение предполагает такие этапы:

1 Этап. Выбираем систему базисных функций 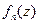, по которой раскладывается предполагаемое решение:

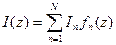(8.4.1.)

Коэффициенты разложения 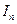называются базисными коэффициентами. В качестве базисной системы можно выбрать разнообразные функции, например:

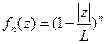(8.4.2.)

- эта функция удовлетворяет граничным условиям на концах антенны (т.е. при 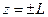, рис. 8.3.5). Функции, отличные от нуля на всем интервале существования тока называются базисными функциями полной области. Помимо них, можно использовать базисные функции, отличные от нуля только на некотором интервале, меньшем, чем 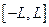. В этом случае говорят о базисных функциях подобластей. Распространенным базисом подобластей для решения задач вибраторных излучателей является кусочно-синусоидальный базис.

Рис. 8.3.5.

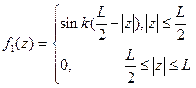, (8.4.3.)

, . ()

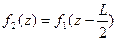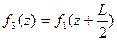Графики этих функций и распределение тока представлены на рис.8.3.6. Из рисунков видно, что в этом случае граничные условия на концах также выполняются автоматически.

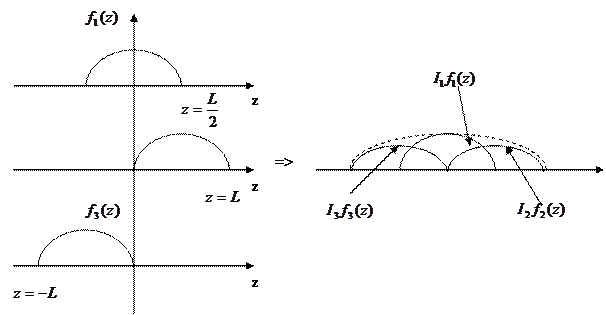
Рис. 8.3.6.

Конкретный вид базисных функций выбирается с учетом физического содержания задачи, выполнения требований граничных условий и быстрой сходимости решения. Типы базисных функций для решения задач электродинамики далеко не ограничивается видом (8.4.2.) или (8.4.3.).Выбор вида базисных функций имеет большое значение, так как от этого зависит число членов N в разложении (8.4.1) и, следовательно, порядок СЛАУ. В конечном счете, от этого зависит время решения на ЭВМ. Примерами базисных функций полной области являются синусоидальные функции, функции Чебышева, степенные функции и т.д. Среди базисных функций подобластей следует выделить кусочно-постоянные (импульсные), кусочно-линейные, кусочно-синусоидальные и другие. Подробнее с представлениями решений в виде разложений по перечисленным базисам можно познакомиться в [4].

2 Этап. Подставляя разложение (8.4.1) в исходное интегральное уравнение (8.3.3) и меняя порядок суммирования и интегрирования, получаем:

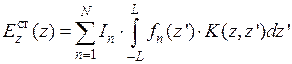(8.4.4)

Таким образом, интегральное уравнение (8.3.3.), сформулированное относительно функции распределения тока заменяется на уравнение (8.4.4), относительно 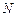неизвестных комплексных коэффициентов (базисных коэффициентов). Уравнение (8.4.4) в таком виде неразрешимо, необходимо иметь 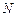условий. Для получения этих условий реализуется процедура Галеркина.

3 Этап. На этом этапе выполняется алгебраизация, т.е. сведение исходного уравнения к системе линейных алгебраических уравнений (СЛАУ). Для этого выбирается система так называемых весовых (проекционных) функций 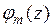, 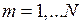. В частном случае она может совпадать с системой базисных функций 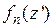. Такая разновидность метода моментов носит название метода Галеркина. Затем, для формирования СЛАУ обе части уравнения (8.4.4) последовательно умножаются на 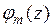для всех 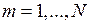, и интегрируются по длине антенны. В результате получаем алгебраическую систему:

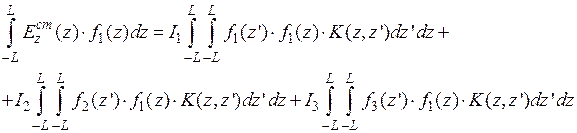
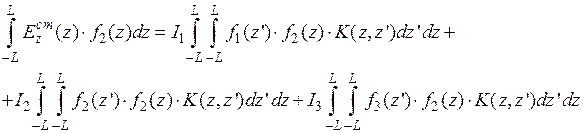
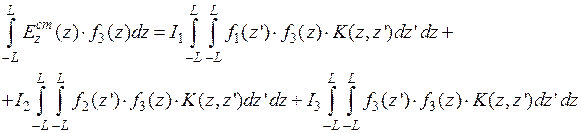
Приведенную систему уравнений можно записать в более лаконичном виде:

,

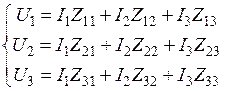где 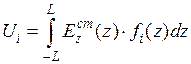, (8.4.5)

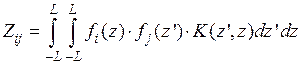, (8.4.6)

В матричной форме полученное СЛАУ примет следующий вид:

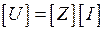. (8.4.7)

В качестве функций 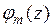могут быть выбраны, например, дельта-функции вида: 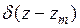. Практически это означает, что интегральное уравнение должно удовлетворяться только в отдельных точках интервала (длины антенны). Этот случай называется методом сшивания в точках или методом коллокации. При большом числе точек сшивания, равномерно распределенных по всей области интегрирования, реше­ние приближается к точному. Преимущество метода коллокации зак­лючатся в простоте вычислений внутреннего интеграла в выраже­нии (8.4.6). Далее следует решать систему (8.4.5) относительно неизвестных базисных коэффициентов 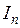и, затем, подставив их в выражение (8.4.1), можно восстановить искомое распределение тока в явном виде. Физический смысл деления вибратора на отрезки при задании на каждом отрезке формы распределения тока, соответствующей форме базисной функции, и последующей алгебраизации интегрального уравнения сводится к замене исходной антенны системой перекрывающихся коротких парциальных элементов (сегментов), которые взаимодействуют друг с другом. В результате взаимодействия в системе установились определенные амплитуды токов в каждом сегменте (соответствующие найденным базисным коэффициентам). Таким образом, фактически установлено соответствие между исходной непрерывной антенной системой и ее дискретными составными частями.

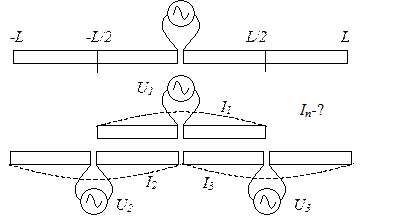
Рис.8.3.7. Геометрия исходной и ее аппроксимация сегментами.

Вычисление интегралов в левой части системы (8.4.7) уравнений не составляет труда: подставляя в выражение стороннее воздействие и соответствующую базисную функцию и воспользовавшись фильтрующим свойством дельта функции можно записать:

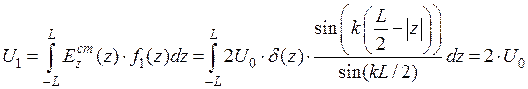, (8.4.8)

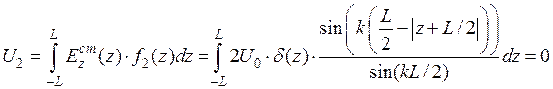, (8.4.9)

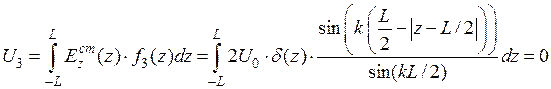, (8.4.10)

Вычисление взаимных импедансов в (8.4.7) представляет собой наиболее трудоемкую процедуру, на которую уходит основная часть машинного времени при численном решении интегрального уравнения. Удается путем двукратного применения процедуры интегрирования по частям свести двойные интегралы в СЛАУ (8.4.7) к однократному. Не повторяя подробно этот вывод, который можно найти в [Марков], приведем окончательный результат:

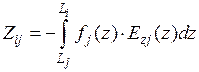, (8.4.11)

где ,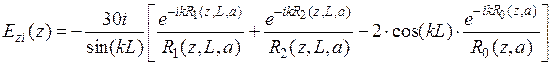

,,

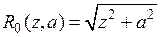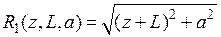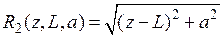
Теперь перейдем к упрощению матрицы правых частей СЛАУ с учетом симметрии исходной задачи.

Очевидно, что для симметричной вибраторной антенны в силу очевидного соотношения 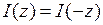базисный коэффициент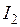, определяющий ток, протекающий по левому сегменту, равен коэффициенту правого .

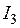Кроме того, в силу одинакового разбиения правого и левого плеча вибраторной антенны можно утверждать, что электромагнитное взаимодействие ряда сегментов одинаковое, в частности:

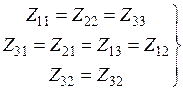, (8.4.12)

Учитывая эти особенности систему уравнений можно существенно упростить, оставив лишь два уравнения с двумя неизвестными:

, (8.4.13)

4 Этап. Выполняется решение СЛАУ.

Из приведенной системы уравнений можно определить базисные коэффициенты в явном виде через коэффициенты СЛАУ:

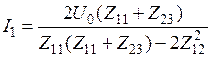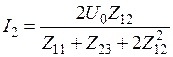, (8.4.14)

5 Этап. Восстановление искомой функции распределения тока и нахождение по нему основных характеристик антенны.

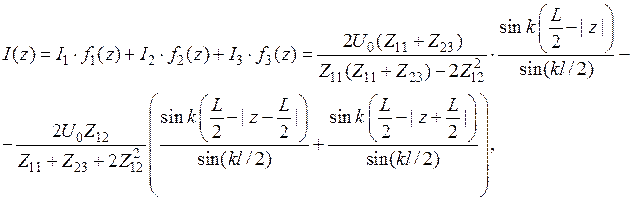
По найденному токовому распределению, на основе ранее найденного соотношения (4.2.) легко найти диаграмму направленности, которая будет комбинацией трех функций с теми же коэффициентами.

Выражение для входного импеданса антенны можно записать в явном виде:

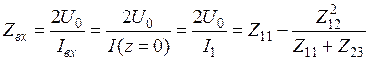(8.4.15)