2014-02-17
704
Списки ребер.
Представление произвольного графа с помощью списка ребер состоит в заполнении массива, содержащего все пары вершин, представляющие ребра графа. Недостатком такого способа представления является возможность утраты информации об изолированных вершинах.
Пусть G = (V, U) - это граф с вершинами V = {Vi,... Vn}. Тогда матрицей смежности этого графа называется квадратная таблица размером n x n, строки и столбцы которой поставлены во взаимно однозначное соответствие вершинам множества V.
Значение элемента этой матрицы, расположенного на пересечении i -и строки и j-го столбца определяется по правилу:
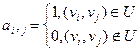(11)
Для графа, изображённого на рисунке 11, матрица смежности имеет следующий вид:
| a | b | c | d | e | v | |
| a | ||||||
| b | ||||||
| c | ||||||
| d | ||||||
| e | ||||||
| v |
