В некоторых случаях табличное представление графа должно сохранять информацию о наименованиях ребер, соединяющих вершины графа. Такая информация отсутствует в представлении графов матрицами смежности. Для сохранения данных об обозначениях ребер можно использовать представление графов матрицами инциденций.
Пусть G = (V, U) - произвольный граф, для которого:
V= {V,,... Vn}- список вершин, U = {U1,...,Uk}- список рёбер.
Тогда матрицей инциденций этого графа называется таблица, имеющая n строк, соответствующих вершинам из V, и k столбцов, соответствующих ребрам из U.
Значение элемента 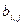 этой матрицы, находящегося на пересечении i-й строки и j-го столбца, определяется по правилу:
этой матрицы, находящегося на пересечении i-й строки и j-го столбца, определяется по правилу:
|
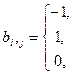
Рассмотрим пример составления матрицы инцидентности для графа, изображённого на рисунке 12.

Рисунок 12 –Ориентированный граф.
Матрица инцидентности.
| A | B | C | D | E | F | G | H | L | K | |
| -1 | ||||||||||
| -1 | ||||||||||
| -1 | ||||||||||
| -1 | ||||||||||
| -1 | ||||||||||
| -1 | -1 | -1 | ||||||||
| -1 |
К недостаткам представления графов матрицами относится большой размер представления по отношению к объему информации, содержащейся в таблицах. Во многих случаях значительная часть информации, содержащейся в матрицах, может оказаться избыточной и использоваться только для поддержания табличной структуры представления графов.
 2014-02-17
2014-02-17 826
826

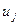 выходит из вершины
выходит из вершины 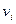 Если ребро
Если ребро 






