2014-02-17
3834
1.8.1. Поле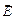
прямолинейного отрезка нити (см. ОРОКС, примеры 1.9, 1.10) (Пример 1).
Найти напряженность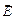электрического поля, созданного отрезком тонкой, однородно заряженной с линейной плотностью 
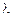нити (см.рис). Углы a1, a2 и расстояние r известны.
Отрезок разбивают на небольшие отрезки, каждый из которых относительно точки наблюдения можно считать точечным.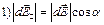 
; 
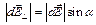
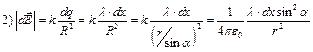
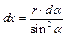
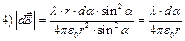
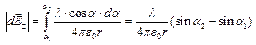
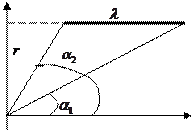
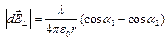
Случай полубесконечной нити;
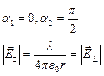
Случай бесконечной нити: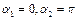
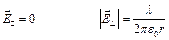
1.8.2. Поле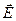 
электрического точечного диполя (Пример 2).
Электрический диполь – система, состоящая из двух одинаковых по величине, но разноименных точечных зарядов +q и –q, расположенных на конечном расстоянии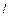 
друг от друга.
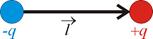
Характеризуется дипольным моментом: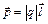 
, направленным от - q к + q.
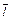– радиус вектор положительного заряда относительно точки, в которой сосредоточен отрицательный заряд
Элементарным или точечным диполем называется предельная система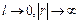 
при конечном p. Расстояние l много меньше расстояния r до точки, где определяется поле системы.
Поле точечного диполя полностью определяется его дипольным моментом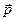 
, тогда как в поле реального диполя заметный вклад дают еще и мультипольные моменты. Поле точечного диполя и поле обычного диполя с одинаковыми дипольными моментами – это поля разные. Поле реальной системы особенно отлично вблизи зарядов.
В электростатике на больших расстояниях поле реального диполя не отличается от поля точечного диполя. Попробуем эту задачу все-таки усложнить. Мы рассматриваем систему из двух точечных зарядов и на некотором расстоянии от этих точечных зарядов мы хотим найти напряженность электрического поля. Точка наблюдения характеризуется радиус-вектором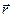 
.
● Напряженность поля в точке, расположенной на оси диполя.
Сначала смотрим этот диполь, когда точка наблюдения расположена на линии дипольного момента.
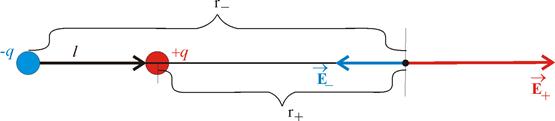
Если расстояние от +q до точки наблюдения обозначить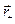 
, а от минуса 
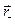, то напряженность поля созданного в точке наблюдения плюсом будет изображаться довольно длинным вектором, а поле созданное в этой же точке, но минусом, будет не только направлено в другую сторону, но еще и вектор 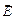будет короче. Наша задача найти суперпозицию.
:
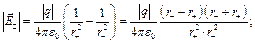
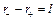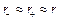так как далеко находимся
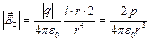
Мы получили составляющую поля напряженности точечного диполя, параллельную линии, соединяющей диполь и точку наблюдения (параллельную вектору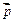 
).
Мы получили скалярное выражение, а можем сделать векторное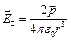 
.
● Напряженность поля диполя в точке, лежащей на перпендикуляре, восстановленном к его середине.
Теперь наша задача в том, чтобы найти составляющую вектора напряженности, действующую на точку, находящуюся на перпендикуляре (в нашем случае – серединном, хотя это и не принципиально, т.к. диполь – точечный) к вектору .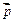
Будем рассматривать единичный положительный пробный заряд, находящийся на расстоянии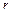 
от диполя (см. Рисунок). Рассматривая соответствующие треугольники (напряженностей и расстояний), получим соотношение:
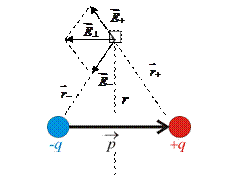
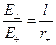
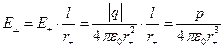
Из рисунка видно, что вектора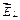 
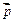и противонаправлены,
поэтому можем записать: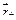 
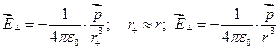
Теперь мы можем найти вектор напряженности поля диполя в любой точке пространства:
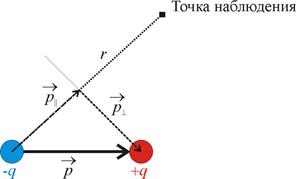
Рассмотрим достаточно произвольную точку пространства, соединим эту точку (обозначенную на рисунке квадратиком) и диполь пунктирной линией. Разложим вектор 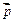на две составляющие: 
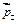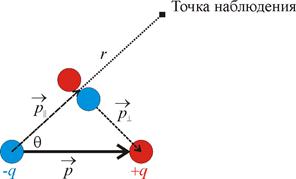
и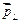 
так, как это показано на Рисунке 1. Если представить диполь в виде полюсов, положительного и отрицательного, то это все равно, что мы в точку наблюдения поместим 2 заряда, положительный и отрицательный, равные по модулю и противоположные по знаку (Рисунок 2). Т.е. получили как будто бы еще 2 диполя - 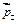и .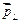
|
|
Итак, напряженность поля диполя можно представить в виде суммы двух его составляющих:
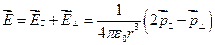
Видно, что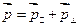 
, 
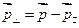
Еще заметим, что 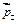можно представить в виде: 
, 
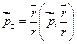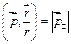
Тогда воспользуемся следующей системой уравнений и подставим эти уравнения в выражения для напряженности, полученные выше:
(*)
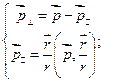
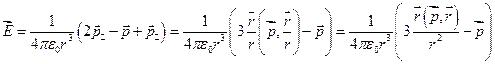По этой формуле может быть найдена напряженность поля точечного диполя в произвольной точке пространства.
