Допустим, в евклидовом пространстве V заданы два базиса  и
и 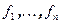 . Обозначим через
. Обозначим через 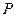 матрицу перехода, связывающие координаты вектора в разных базисах. Пусть для определённости
матрицу перехода, связывающие координаты вектора в разных базисах. Пусть для определённости 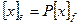 . Скалярное произведение не зависит от выбора базиса, поэтому
. Скалярное произведение не зависит от выбора базиса, поэтому 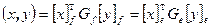 . Подставим в правую часть равенства вместо координат вектора в базисе e их выражение через координаты в базисе f. В результате придём к равенству
. Подставим в правую часть равенства вместо координат вектора в базисе e их выражение через координаты в базисе f. В результате придём к равенству 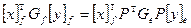 . Поскольку полученное равенство справедливо для любых векторов x и y, то выводим
. Поскольку полученное равенство справедливо для любых векторов x и y, то выводим 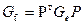 .
.
Изменение матрицы Грама при изменении базиса
|
|

Сейчас читают про:
 2014-02-17
2014-02-17 772
772







