Пучок матриц

Пусть даны квадратичные формы 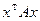и 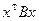. Рассмотрим пучок квадратичных форм 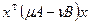. Если квадратичные формы 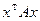и 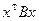заменой координат x=Py приводятся к каноническому виду, то все формы из пучка 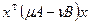приводятся к каноническому виду этой же заменой координат. Пусть 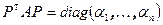и 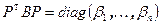, тогда 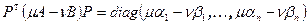. Из последнего равенства выводим 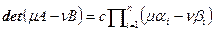, то есть многочлен 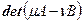раскладывается на линейные множители над полем вещественных чисел. Из равенства 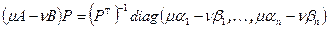выводим, что i -ый столбец матрицы P удовлетворяет однородной системе уравнений 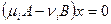. Таким образом, получается следующий алгоритм приведения пары квадратичных форм к нормальному виду.

1. Раскладываем многочлен 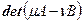на линейные множители. Если разложения не существует, то искомой замены координат не существует.
2. Для каждого линейного множителя 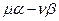многочлена 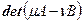находим базис подпространства 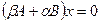. Если размерность подпространства меньше кратности множителя, то искомой замены координат не существует. В противном случае, будет построен базис, в котором квадратичные формы имеют нормальный вид.

Для обоснования этого подхода требуется показать, что объединение линейно независимых систем векторов, соответствующих разным линейным множителям, образует линейно независимую систему. Доказательство проводится также как и для собственных векторов.