Теорема об изменении количества движения
Уравнение движения точки переменной массы.
При полете ЛА с работающим реактивным двигателем происходит отбрасывание от него продуктов сгорания (ПС) топлива. А в случае, если на ЛА установлен воздушно-реактивный двигатель, то кроме отбрасывания ПС топлива на ЛА поступают все новые и новые частицы воздуха, т.е. состав (масса) ЛА в процессе полета непрерывно меняется.
Рассматривая движение ЛА удобно в каждый момент времени включать в его состав только те частицы, которые в данный момент времени находятся внутри объема ЛА. При такой постановке ЛА с работающим двигателем представляет собой систему переменного состава, к которой непосредственно нельзя применить теоремы динамики твердого тела.
Однако основываясь на этих классических теоремах И.В.Мещерский доказал аналогичные теоремы для системы материальных точек переменной массы и установил принцип составления уравнений движения реактивного ЛА.
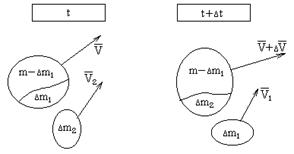 Будем считать, что масса интересующего нас объекта в какой-то промежуток времени
Будем считать, что масса интересующего нас объекта в какой-то промежуток времени 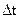 будет изменяться за счет отсоединения и присоединения масс частиц. Допустим, что в какой-то момент времени t частица массой m движется со скоростью V.
будет изменяться за счет отсоединения и присоединения масс частиц. Допустим, что в какой-то момент времени t частица массой m движется со скоростью V.
Используем теорему об изменении количества движения системы материальных точек на промежутке времени 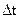 .
.
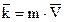 - количество движения;
- количество движения;
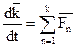 - сумма внешних сил.
- сумма внешних сил.
| Масса | Количество движения | |
| t | 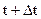
| |
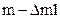
| 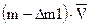
| 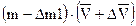
|
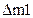
| 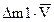
| 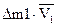
|
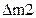
| 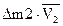
| 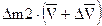
|
Определим приращение количества движения системы материальных точек за промежуток времени 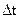 .
.
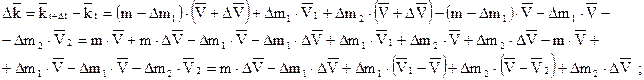
Рассмотрим предел:
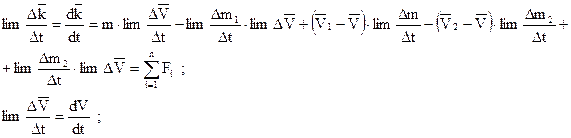
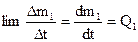 - расход топлива;
- расход топлива;
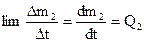 -приход топлива;
-приход топлива;
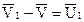 -относительная скорость отсоединения частиц;
-относительная скорость отсоединения частиц;
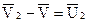 - относительная скорость присоединения частиц.
- относительная скорость присоединения частиц.
Таким образом получили уравнение:
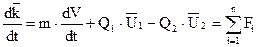 ;
;
Уравнение Мещерского для поступательного движения тела переменной массы:
 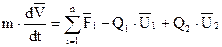
|
 2014-02-17
2014-02-17 645
645








