Коэффициент температурного расширения
Коэффициент температурного расширения b t (0С)-1, выражает относительное изменение объема жидкости при изменении температуры на один градус:
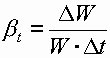 ,
,
где D W - изменение объема W, соответствующее изменению температуры на величину D t.
Коэффициент температурного расширения воды увеличивается с возрастанием температуры и давления; для большинства других капельных жидкостей b t с увеличением давления уменьшается
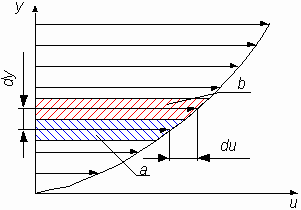
| Вязкостью называется свойство жидкости оказывать сопротивление перемещению одной части жидкости относительно другой. Вязкость проявляется только при движении жидкости и сказывается на распределении скоростей по живому сечению потока (рис. 1.1). |
Согласно гипотезе Ньютона сила внутреннего трения F в жидкостях пропорциональна градиенту изменения скорости 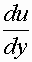 , площади соприкосновенияслоев S, зависит от рода жидкости и очень незначительно зависит от давления.
, площади соприкосновенияслоев S, зависит от рода жидкости и очень незначительно зависит от давления.
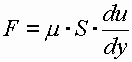 ,
,
где S - площадь соприкасающихся слоев, м2; du - скорость смещения слоя " b " относительно слоя " a ", м/с; dy - расстояние, на котором скорость движения слоев изменилась на du, м;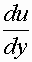 - градиент скорости, изменение скорости по нормали к направлению движения (с-1); m - коэффициент динамической вязкости (Па? с).
- градиент скорости, изменение скорости по нормали к направлению движения (с-1); m - коэффициент динамической вязкости (Па? с).
Если силу трения F отнести к единице площади соприкасающихся слоев, то получим величину касательного напряжения t
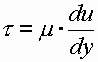 .
.
При градиенте скорости 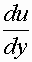 = 1; m = t и выражает силу внутреннего трения, приходящуюся на единицу площади поверхности соприкасающихся слоев жидкости.
= 1; m = t и выражает силу внутреннего трения, приходящуюся на единицу площади поверхности соприкасающихся слоев жидкости.
В практике для характеристики вязкости жидкости чаще применяют не коэффициент динамической вязкости, а коэффициент кинематической вязкости n (м2/с). Коэффициентом кинематической вязкости называется отношение коэффициента динамической вязкости к плотности жидкости:
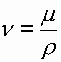 .
.
Вязкость жидкости зависит от рода жидкости, от температуры и от давления.
СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЖИДКОСТЬ
Силы, действующие на жидкость можно разделить на две группы: внутренние и внешние.
Внутренние силы - силы взаимодействия между частицами жидкости.
Внешние – силы, приложенные к частицам рассматриваемого объёма со стороны других тел.
Внешние силы, в свою очередь, делятся на массовые и поверхностные.
Поверхностные силы приложены к отдельным частицам, находящимся на поверхности раздела. Пропорциональны площади поверхности, на которую действуют. Передаются от частицы к частице без изменения. Например, атмосферное давление, действующее на свободную поверхность, а также силы трения.
Массовые силы - эти силы действуют на все частицы, рассматриваемого объема, величина сил пропорциональна массе этих частиц. Передаются от частицы к частице, суммируясь.
ГИДРОСТАТИКА
Изучает законы давления жидкости на плоскости и криволинейные поверхности, и законы равновесия плавающих тел.
ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ И ЕГО СВОЙСТВА
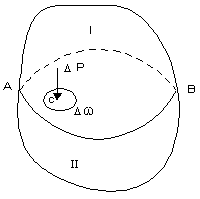
| Гидростатическое давление - это сжимающее напряжение, которое возникает в жидкости находящейся в состоянии относительного покоя. 1 свойство: Гидростатическое давление действует нормально к площадке действия и является сжимающим, т.е. оно направлено внутрь того объема жидкости, который рассматриваем. 2 свойство: Гидростатическое давление в данной точке не зависит от направления. 3 свойство: Гидростатическое давление есть функция координаты. |
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ ЖИДКОСТИ
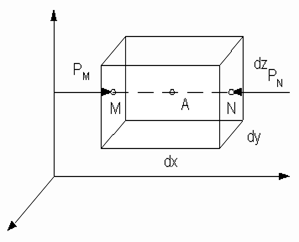
| Рассмотрим равновесие жидкости. В объеме жидкости произвольно проведем систему координат. Выделим некоторую точку А. Вокруг, которой проведем бесконечно малый параллелепипед. Рассмотрим внешние силы, действующие на этот параллелепипед.
1. массовые силы
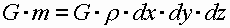 проекция на ось х
проекция на ось х 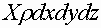
|
2. поверхностные силы

Сумма проекций всех сил на ось х
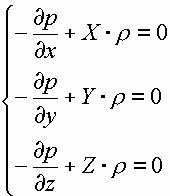
ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Умножим каждое из уравнений соответственно на dx, dy и dz и просуммируем.
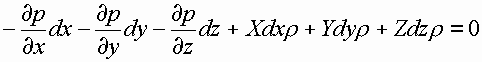
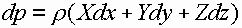
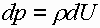
Проинтегрируем

Введем граничные условия 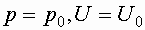 , тогда
, тогда
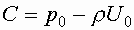
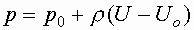
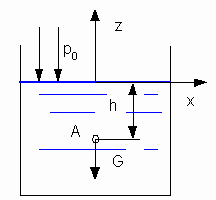
| Рассмотрим частный случай, когда на жидкость действует только сила тяжести. Проведем оси координат по поверхности жидкости. Проекции массовых сил будут следующими X=0, Y=0, Z=-g |
Тогда
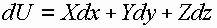
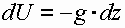
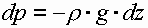
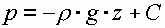
p=p0 –z=h
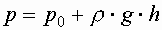
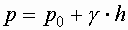
ПЬЕЗОМЕТРИЧЕСКАЯ ВЫСОТА
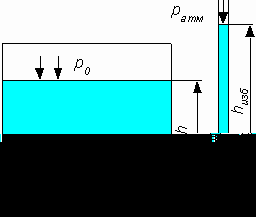
| Рассмотрим закрытый резервуар не полностью заполненный жидкостью давление, на свободной поверхности которого больше атмосферного. Подключим к т. N тонкую открытую стеклянную трубку – пьзометр благодаря действию давления в т. N уровень жидкости в трубке поднимется на некоторую высоту hизб. Со стороны жидкости в сосуде давление в т. N равно |
Со стороны жидкости в трубке давление в т. N
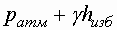
Так как давления в т. N слева и справа равны можно записать
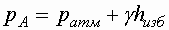 или
или 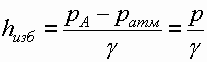
Высота hизб называется пьзометрической высотой
ВАКУУМ
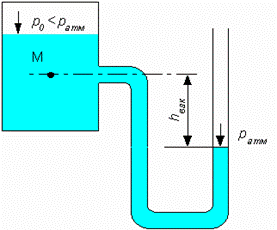
| Рассмотрим закрытый резервуар не полностью заполненный жидкостью давление, на свободной поверхности которого меньше атмосферного. Подключим к т. M обратный пьзометр. Очевидно, что в этом случае уровень жидкости в пьзометре опустится ниже уровня жидкости в резервуаре
Со стороны жидкости в сосуде давление в т. M равно
|
Со стороны жидкости в трубке давление в т. M
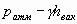
Так как давления в т. M слева и справа равны можно записать
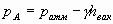 или
или 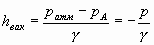
Высота hвак называется вакуумметрической высотой. Вакуумметрическая высота характеризует разность атмосферного и абсолютного давлений. Именно эта разность, а не само давление называется вакуумом. Вакуум в данной точке есть недостаток давления до атмосферного.
УДЕЛЬНАЯ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ПОТЕНЦИАЛЬНЫЙ НАПОР.
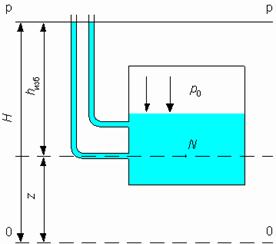
| Жидкость, находящаяся в покое или движении обладает определенным запасом энергии. Покоящаяся жидкость обладает потенциальной энергией. Подключим к т. N открытый пьезометр. Под действием избыточного давления в т. N объем жидкости весом G поднимется на высоту hизб над плоскостью NN и на высоту H над плоскостью ОО. |
Рассматриваемый объем может произвести работу.
1. За счет падения на плоскость ОО с высоты z. Эта работа будет равна Ez= z G.
2. За счет поднятия под давлением p на высоту hизб
Ep= hизб G.
Полная работа, таким образом, которую может произвести объем жидкости весом G
E = Ez + Ep = z G + hизб G
Удельной потенциальной энергией - называется энергия, отнесенная к единице веса
e = E / G = z + hизб= H.
Как видно, удельная потенциальная энергия состоит из удельной потенциальной энергии положения z и удельной потенциальной энергии давления hизб = p / g.
Потенциальный напор - удельная потенциальная энергия, т.е. энергия которой обладает единица веса жидкости
H = z +hизб
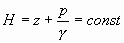
Необходимо запомнить отличие давления от напора.
Напор - удельная энергия - величина постоянная для данного объема жидкости.
Давление - сжимающее напряжение, зависящее от координаты точки.
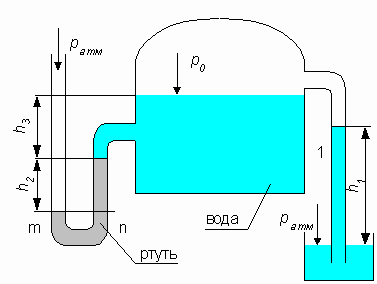
| Определить давление в резервуаре  и высоту подъема уровня и высоту подъема уровня 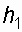 в трубке 1, если показания ртутного манометра в трубке 1, если показания ртутного манометра 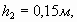 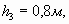 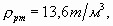 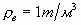 .
Решение:
Запишем условия равновесия для ртутного манометра для плоскости
а) со стороны резервуара .
Решение:
Запишем условия равновесия для ртутного манометра для плоскости
а) со стороны резервуара 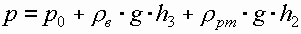
|
б) со стороны манометра 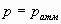 , тогда
, тогда
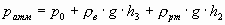
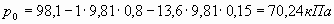
Таким образом, в резервуаре - вакуум, величина которого равна:
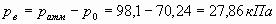
Условия равновесия трубки 1
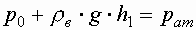
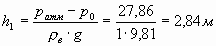
СИЛА ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ, ДЕЙСТВУЮЩАЯ НА ПЛОСКУЮ ФИГУРУ
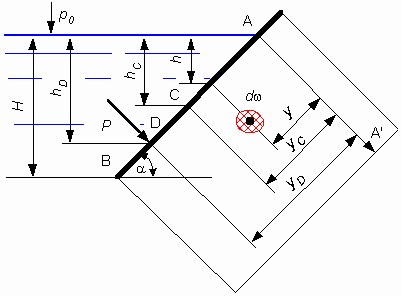
1. Найти величину силы абсолютного гидростатического давления.
2. Найти положение линии действия силы.
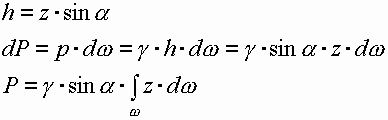
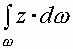 - статический момент площади.
- статический момент площади. 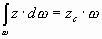
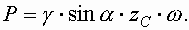
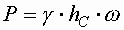
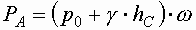
Сила гидростатического давления, действующая на плоскую фигуру любой формы равна площади этой фигуры умноженной на гидростатическое давление в центре тяжести этой фигуры.
Разложим силу PA на Pатм и Р. Центр действия силы Ратм будет совпадать с центром тяжести фигуры, поскольку атмосферное давление равномерно распределяется по поверхности. Центр действия силы Р будет расположен ниже, т.к. избыточное давление зависит от глубины погружения.
Искомая сила РА является геометрической суммой сил Pатм и Р.
Сумма моментов составляющих сил равна моменту равнодействующей силы
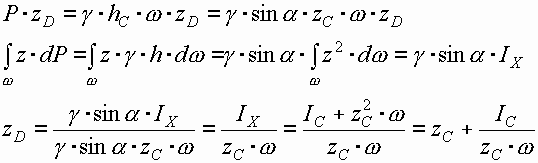
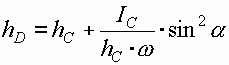
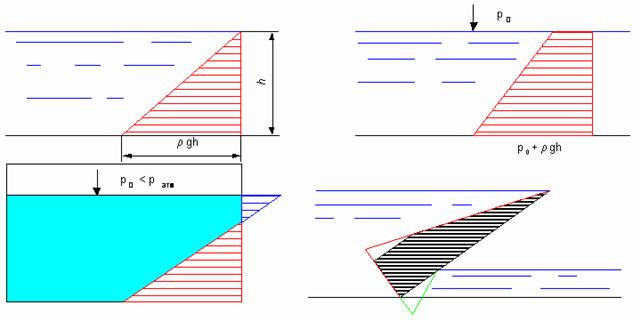
ГРАФОАНАЛИТИЧЕСКИЙ СПОСОБ
 2014-02-18
2014-02-18 839
839







