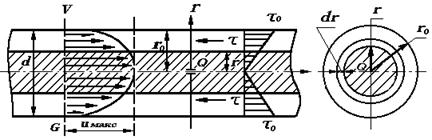
Исследуем ламинарный режим движения жидкости теоретически.
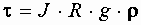
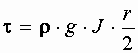
r = 0 t = 0
r = r0 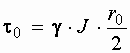
Из последнего выражения виден линейный закон изменения касательного напряжения по сечению.
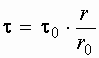
С другой стороны

Следовательно
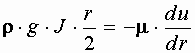
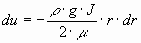
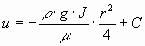
Постоянная интегрирования 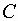 определяется из условия равенства нулю скорости
определяется из условия равенства нулю скорости 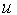 у стенок трубы при
у стенок трубы при 
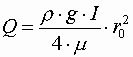 .
.
Окончательно, подставив значение 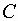 в уравнение (1.6) получим уравнение, выражающее закон распределения скоростей при ламинарном режиме
в уравнение (1.6) получим уравнение, выражающее закон распределения скоростей при ламинарном режиме
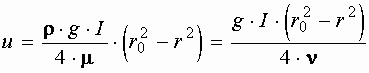
где 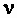 - коэффициент кинематической вязкости.
- коэффициент кинематической вязкости.
Уравнение, известное как формула Стокса, представляет уравнение параболы, имеющей максимум при 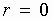 , то есть по оси трубы
, то есть по оси трубы
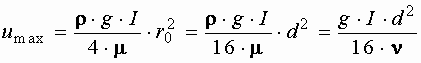
Зная закон распределения скорости по живому сечению трубы, получим зависимость для определения расхода
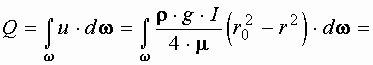
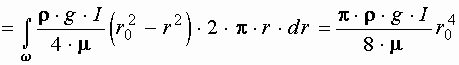 .
.
Зависимость, определяющая расход носит название формулы Пуазейля.
Так как 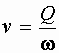 , получаем
, получаем
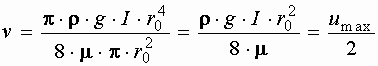 ,
,
то есть средняя скорость в трубе при ламинарном режиме равна половине максимальной скорости, наблюдаемой на оси. Преобразуем зависимость
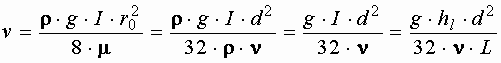 ,
,
откуда
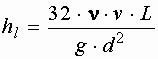 ,
,
где 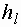 - потери напора по длине.
- потери напора по длине.
Зависимость, определяющая величину потерь напора при ламинарном режиме движения, показывает, что потери напора при ламинарном режиме пропорциональны первой степени средней скорости, зависят от рода жидкости, обратно пропорциональны площади сечения трубы и не зависят от шероховатости стенок трубы.
Преобразуем зависимость, умножив числитель и знаменатель на 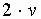 и перегруппировав сомножители
и перегруппировав сомножители
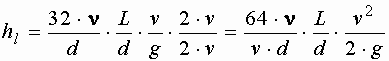 .
.
 2014-02-18
2014-02-18 755
755








