Доказательство. Если корень имеет чётную кратность, то на границах бесконечно малого отрезка с центром в этом корне функция имеет одинаковые знаки

Доказательство.

Следствие 2.

Следствие 1.

Если корень имеет чётную кратность, то на границах бесконечно малого отрезка с центром в этом корне функция имеет одинаковые знаки.

Если корень имеет нечётную кратность, то на границах бесконечно малого отрезка с центром в этом корне функция имеет разные знаки.

Пусть на заданном отрезке [a,b] лежит 1 корень чётной кратности, тогда в силу следствия 1 на границах отрезка знак меняться не будет, что означает остановку выполнения итераций и недостижение необходимой точности. Если же на отрезке [a,b] лежит 1 чётно кратный корень и 1 нечётно кратный корень, то чётно кратный корень будет просто игнорирован методом, т.к. условие смены знака являющееся также основным условием, с помощью которого определяется корень на текущем полуотрезке, в силу следствия 1 не выполнится. Следовательно, чётно кратный корень не может быть найден с помощью данного метода.

█

Утверждение 2. Если на концах начального отрезка значения функции имеют один знак, то метод может не сойтись, то есть, возможно, ни один из корней не будет найден с заданной точностью.

Первым вариантом постоянства знака функции на границах отрезка является отсутствие корня на нём, поэтому исключим этот случай как тривиальный, будем считать, что на отрезке хотя бы один корень существует. Вторым вариантом – существование чётного количества корней.

Если f(a)f(b)³0, то продолжать итерации невозможно, т.к. условие смены знака не подтверждается. Если же, тем не менее, на первом шаге не проверять условие смены знака и разделить отрезок пополам, то может возникнуть ситуация, в которой корни распределяться по чётному количеству в каждой половине отрезка. А чётное количество корней означает чётное количество пересечений оси Ox, даже если существуют кратные корни.

Следовательно, условие смены знака вновь не подтвердится для обеих половинок исходного отрезка. Следовательно, дальнейшие итерации не будут выполнены, и не будет достигнута заданная точность.

█

Утверждение 3. Если на концах начального отрезка значения функции имеют разные знаки, то будет найден с заданной точностью один из корней лежащих на нём.

В силу утверждения 1 будем рассматривать только корни нечётной кратности. Так как функция меняет знак на концах отрезка, предположим, f(a)≥0, f(b)≤0. Тогда если f(x_c)≥0, то для дальнейшего приближения выберем отрезок [x_c,b], т.к. f(b)f(x_c)≤0. Если же f(x_c)≤0, то для дальнейшего приближения выберем отрезок [a,x_c], т.к. f(a)f(x_c)≤0. Для второго случая, когда f(a)≤0, f(b)≥0 аналогично доказывается существование одного из полуотрезков, на котором функция меняет знак. Из чего следует, что после каждой итерации для одного из полуотрезков условие смены знака обязательно будет выполнено. Следовательно, нет причин для остановки итерационного процесса, который завершится лишь по достижении заданной точности.

█

Построим блок-схему алгоритма вычисления корня уравнения вида (1) с помощью метода дихотомии. Пусть на начальном отрезке [a,b] функция меняет знак, т.е. на этом отрезке существует нечётное количество нечётно кратных корней. Пример такой функции изображён на рис. 1. Необходимо найти корень x_т с точностью ε. Будем считать x_т точным значением корня, x_ч – значение корня полученное данным методом, тогда задача считается выполненной, если x_чÎ[x_т-ε,x_т+ε].

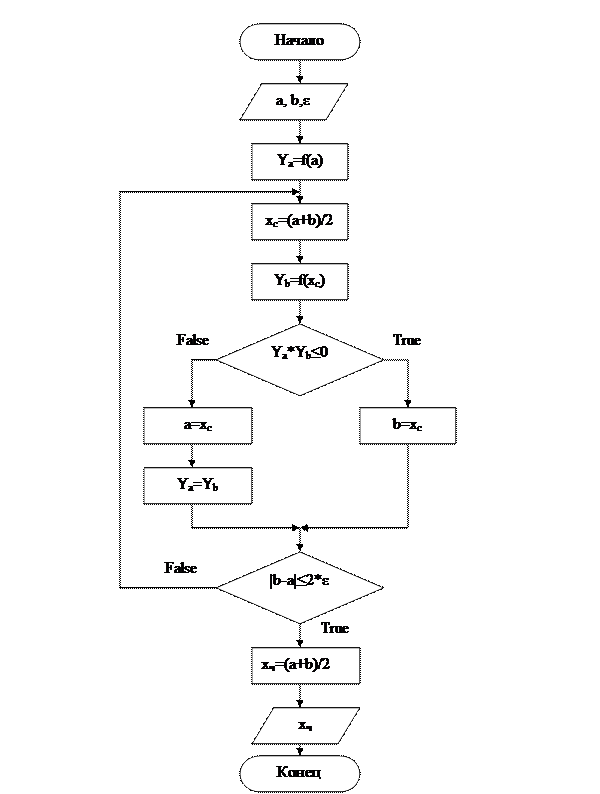
Дихотомия применяется тогда, когда требуется высокая надежность счета, а скорость сходимости малосущественна.

Метод простых итераций

Основной принцип метода заключается в том, что уравнение (1) представляется в виде:

x=φ(x), (4)

где φ(x) можно определить многими способами, например, так:

φ(x)=x-αf(x), α=const, или

φ(x)=x+ψ(x)f(x),

где ψ(x) – произвольная, непрерывная, знакопостоянная функция на отрезке [a,b].

Метод простых итераций в силу (4) определяется следующей рекурсивной формулой:

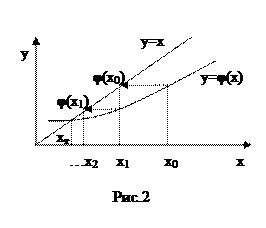x_n+1=φ(x_n), где n= 0,1,2,… (5)

Здесь n имеет смысл номера итерации, x₀ – некоторое начальное приближение. Из (5) видно, что если x_n→x_т, то этот предел и есть корень уравнения (рис. 2).

Пусть в окрестности точки x_т (x_т-Δ,x_т+Δ), где Δ>0 функция φ(x) удовлетворяет условию Липшица:

|φ(x₂)-φ(x₁)|≤q|x₂-x₁| (6)

для любых x₂,x₁Î(x_т-Δ,x_т+Δ),

0 <q< 1, (7)

при этом x₀Î(x_т-Δ,x_т+Δ), (8)

причём, (x_т-Δ,x_т+Δ) Î[a,b].

В связи с этим допущением можно сделать несколько утверждений.