Формулы Байеса

Пусть A ₁, A ₂,..., A_n,... конечная или счетная полная система событий, Р (A_i)>0 для любого i и событие В такое, что Р (В) > 0. Тогда при любом i справедливы равенства:

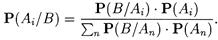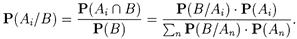Эти формулы называются формулами Байеса. Формулы очевидны, поскольку

Здесь мы воспользовались формулами умножения вероятностей и полной вероятности.

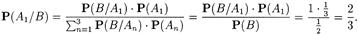Пример 1. В условиях примера 1 из 1.3.2 предположим, что мы вынули золотую монету. Какова вероятность того, что был выбран первый стол? Воспользуемся формулой Байеса.

Пример 2. В условиях примера 2 из 1.3.2 предположим, что поступившая на сборку деталь бракованная. Найдем вероятность того, что эта деталь поступила со второго автомата. По формуле Байеса

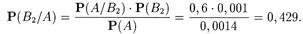Замечание. Формулы Байеса применяются при решении следующей задачи. Пусть до проведения эксперимента имеются n предположений (гипотез) относительно характера эксперимента A ₁, A ₂, …, A_n. При этих предположениях проводится эксперимент. В результате эксперимента произошло событие В. Считаем, что до эксперимента известны вероятности

P (A ₁), P (A ₂), …, P (A_n)

(или их легко можно вычислить). Эти вероятности называются априорными вероятностями гипотез. Известны также вероятности появления события В при условии реализации той или иной гипотезы A_i:

P (B / A ₁), P (B / A ₂), …, P (B / A_n).

Нас интересуют вероятности после эксперимента:

P (A ₁ / B), P (A ₂ / B), …, P (A_n / B),

которые называются апостериорными вероятностями гипотез. Эти вероятности вычисляются по формулам Байеса. Можно считать, что апостериорные вероятности гипотез уточняют априорные, используя информацию, полученную в результате эксперимента.