Что нужно, чтобы n случайных событий можно было назвать независимыми в совокупности?
Во-первых, любые два события должны быть независимыми, т.е.
P (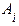 Ç
Ç 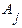 )= P (
)= P (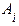 ) × P (
) × P (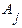 ), i ¹ j
), i ¹ j
Рассмотрим произвольные три события 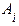 ,
, 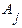 , и
, и 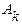 — они должны быть независимыми, т.е.
— они должны быть независимыми, т.е.
Р (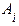 Ç
Ç 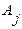 Ç
Ç 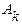 ) = Р (
) = Р (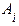 Ç
Ç 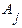 )× P (
)× P (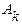 )
)
= P (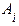 ) × P (
) × P (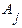 ) × P (
) × P (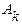 ).
).
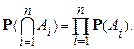 |
Аналогичными рассуждениями получаем, что должно выполняться следующее равенство:
Определение. События 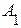 ,
, 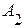 ,...,
,..., 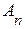 называются независимыми (независимыми в совокупности), если для любого конечного набора из этих событий:
называются независимыми (независимыми в совокупности), если для любого конечного набора из этих событий:
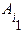 , …,
, …, 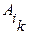 , 1£ i 1 < i 2 <.... < ik £ n, k= 1 ,..., n
, 1£ i 1 < i 2 <.... < ik £ n, k= 1 ,..., n
выполняется равенство
P (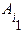 Ç … Ç
Ç … Ç 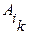 ) = P (
) = P (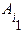 )· … P (
)· … P (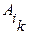 ).
).
Пример. Радист трижды вызывает корреспондента. Вероятность того, что будет принять первый вызов, равна 0,2; второй вызов — 0,3; третий вызов — 0,4. По условиям приема, события, состоящие в том, что данный вызов будет услышан, независимы. Нас интересует вероятность события
А = { корреспондент вообще услышит вызов }.
Обозначим через
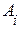 = { корреспондент услышит i - й вызов }, i = 1,2,3.
= { корреспондент услышит i - й вызов }, i = 1,2,3.
Если учесть, что А заключается в том, что корреспондент услышит хотя бы один вызов, то найдем вероятность противоположного события
Ā = { корреспондент не услышит ни одного вызова }.
Так как 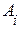 , i = 1,2,3 независимые события, то
, i = 1,2,3 независимые события, то
Р (Ā) = Р (Ā 1 Ç Ā 2 Ç Ā 3)= Р (Ā 1) × Р (Ā 2) × Р (Ā 3)
= (1-0,2)(1-0,3)(1-0,4) =0,336.
Отсюда получим искомую вероятность Р (A) = 0, 664.
 2014-02-18
2014-02-18 3656
3656
