Сначала рассмотрим наиболее важные распределения дискретных случайных величин.
1. Распределение Бернулли с параметром р, 0 < р < 1.
Дискретная случайная величина x имеет распределение Бернулли (или x распределена по закону Бернулли), если она принимает значения 0 и 1 с вероятностями q и р, соответственно. Таблица распределения выглядит так:
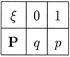 |
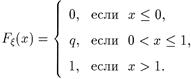 |
Функция распределения x имеет вид (см. 2.2.1.):
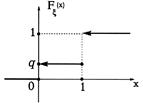 |
График этой функции строится следующим образом
2. Биномиальное распределение с параметрами n, р.
 |
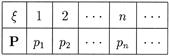
Дискретная случайная величина x распределена по биномиальному закону, если ее таблица распределения выглядит так:
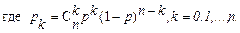 |
Проверьте самостоятельно, что
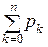 = 1.
= 1.
Число успехов в п экспериментах (одинаковых) двумя исходами в каждом эксперименте является примером случайной величины, имеющей биномиальное распределение.
3. Геометрическое распределение с параметром q, 0 £ q < 1.
 |
Дискретная случайная величина x имеет геометрическое распределение, если ее таблица распределения имеет следующий вид:
где рk = qk- 1 (1 - q), k = 1, 2,..., n,....
Проверьте самостоятельно, что 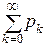 = 1.
= 1.
Число независимых экспериментов, которые необходимо провести до появления первого успеха является примером случайной величины, имеющей геометрическое распределение.
4. Распределение Пуассона с параметром l, l > 0.
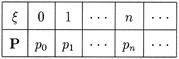 |
Дискретная случайная величина x имеет распределение Пуассона, если ее таблица распределения выглядит следующим образом:
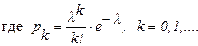 |
Проверьте самостоятельно, что
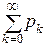 = 1.
= 1.
Примером такой случайной величины является число вызовов, поступивших на телефонную станцию за определенный промежуток времени.
Теперь приведем примеры наиболее важных распределений непрерывных случайных величин.
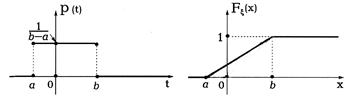
5. Равномерное распределение на отрезке [ a, b ].
Непрерывная случайная величина x имеет равномерное распределение на отрезке [ а, b ], если ее плотность распределения имеет следующий вид:
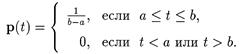 |
Функция распределения такой случайной величины определяется так: если x < a, то { x < х } — невозможное событие, поэтому Fx (x) = 0. Если х > b, то { x < х } — достоверное событие, поэтому Fx (x) = 1. А при а £ х < b получим
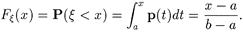 |
Таким образом получаем функцию распределения
Графики плотности распределения p(t) и функции распределения Fx (x) приведены ниже
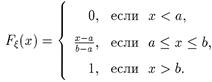 |
6. Показательное (экспоненциальное) распределение с параметром l, l > 0
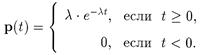 |
Непрерывная случайная величина x имеет показательное распределение, если ее плотность распределения имеет следующий вид:
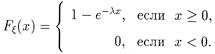 |
Аналогичными рассуждениями из предыдущего пункта получим функцию распределения такой случайной величины:
 |
Графики плотности распределения p [t) и функции распределения Fx (x) приведены ниже
Примерами показательно распределенных случайных величин могут служить: а) время распада атомов различных элементов, б) продолжительность безотказной работы радиоаппаратуры, в) длительность горения электрической лампочки, г) время обслуживания в системах массового обслуживания.
 2014-02-18
2014-02-18 983
983








