2014-02-18
522
Пусть {W, F, Р } —вероятностное пространство, x 1(w), x 2(w), …, xn (w) — заданные на нем случайные величины. Для любого w Î W определим
x (w)=(x 1(w), x 2(w), …, xn (w)),
т.е. упорядоченную последовательность п случайных величин со значениями в Â 1.
Определение 1. Случайным вектором называется отображение
x: W ® Â n
Иногда, x = (x 1, x 2, … xn) называется также многомерной случайной величиной. Здесь x 1, x 2, … xn (проекции вектора x на каждую ось) — случайные величины, заданные на одном и том же вероятностном пространстве {W, F, Р }.
Определение 2. Функцией распределения случайного вектора x называется следующая функция
Fx(x 1, x 2, …, xn)= P (x 1< x 1, x 2< x 2, …, xn < xn).
Функцию Fx(x 1, x 2, …, xn) называют также совместной функцией распределения случайных величин x 1, x 2, … xn. .
В дальнейшем мы в основном будем иметь дело с двумерным случаем. Поэтому мы остановимся на нем, отметив, что n -мерный случай рассматривается аналогично.
Ограничимся перечислением свойств двумерной функции распределения, отметив лишь, что они доказываются аналогично соответствующим свойствам одномерной функции распределения.
1). 0 £ Fx (x 1, x 2) £ 1, для любых (x 1, x 2) Î Â 2.
2). Fx (x 1, x 2) — неубывающая функция по каждому из аргументов x 1, x 2.
3). Fx (-¥, x 2) =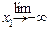 
Fx (x 1, x 2) = 0, Fx (x 1, -¥) = 
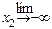Fx (x 1, x 2) = 0,
Fx (- ¥ , -¥) =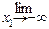 
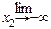Fx (x 1, x 2) = 0,
Fx (+¥ , x 2) = 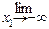Fx (x 1, x 2) = F
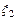(x 2),
Fx (x 1, +¥) = 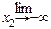Fx (x 1, x 2) = F 
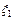(x 1),
Fx (+¥ ,+¥) =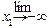 
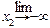Fx (x 1, x 2) = 1.
4). P (a 1£ x1< b 1, a 2£ x2< b 2)= Fx(b 1, b 2)- Fx(b 1, a 2)- Fx(a 1, b 2)+ Fx(a 1, a 2).
5). Fx (x 1, x 2) — непрерывная слева по каждому из аргументов x 1 и x 2 функция.
