Классическая вероятность
Определение. События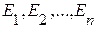 ...образуют полную систему {или группу) событий, если 1)
...образуют полную систему {или группу) событий, если 1) 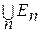 = W; 2)
= W; 2) 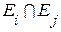 = Æ для i¹ j
= Æ для i¹ j
Пусть события 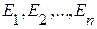 образуют полную систему. Рассмотрим событие А =
образуют полную систему. Рассмотрим событие А =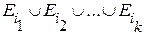 , тогда будем говорить, что событию А благоприятствуют k из п событий
, тогда будем говорить, что событию А благоприятствуют k из п событий 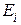 .
.
Теорема. Пусть 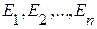 образуют полную систему событий и равновероятны (или равновозможны), и пусть событию А благоприятствуют k из этих п событий, тогда
образуют полную систему событий и равновероятны (или равновозможны), и пусть событию А благоприятствуют k из этих п событий, тогда
P (A) = k/п.
Доказательство. Так как 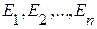 образуют полную систему событий, то
образуют полную систему событий, то 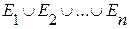 = WТогда, по аксиомам 3 и 2 получаем:
= WТогда, по аксиомам 3 и 2 получаем:
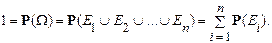
По условию теоремы P (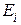 ) — одна и та же для всех i, что нам дает P (
) — одна и та же для всех i, что нам дает P (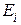 ) = 1 /n для любого i. Поскольку А =
) = 1 /n для любого i. Поскольку А = 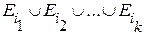 , то по аксиоме 3 получаем P (A) = k/п.
, то по аксиоме 3 получаем P (A) = k/п.
Пример. В урне имеются k белых и n — k красных шаров. Извлекается из урны 1 шар. Какова вероятность того, что этот шар белый? Все исходы равновероятны, их всего п: 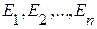 . Событию А = { извлеченный шар белый } благоприятствуют k из n исходов, поэтому из теоремы следует ответ:
. Событию А = { извлеченный шар белый } благоприятствуют k из n исходов, поэтому из теоремы следует ответ:
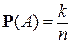 .
.
Применение теоремы из предыдущего пункта ограничивается только случаями, когда число исходов проводимого эксперимента можно перечислить. Как же вычислить вероятности событий, когда этого делать нельзя (т.е. когда множество исходов эксперимента несчетно). В некоторых случаях это можно сделать, пользуясь геометрическим языком. Пусть G Ì Ân некоторая ограниченная область n -мерного пространства. Например, на прямой (в Â1) — это может быть отрезок; на плоскости (в Â2) —прямоугольник и т.д. Предполагается, что область G имеет меру m(G) (длину в Â1, площадь в Â2 и т.д.) такую, что 0 < m(G) < ∞.
В область G наугад бросается точка. Этому выражению следует придать определенный смысл: брошенная точка может попасть в любую точку области G, вероятность попасть в какую либо часть g области G пропорциональна мере этой части и не зависит от ее расположения и формы, т.е. Р( попасть в g) = k×m(g), где k- коэффициент пропорциональности. Тогда Р( попасть в G) = k×m(G) и поскольку событие (попасть в G) — достоверное, то отсюда получим (используя аксиому 2 вероятности): k = 1/ m(G).
Вероятность попасть в g, вычисленная вышеописанным способом, носит название геометрической вероятности и определяется так:
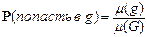 .
.
Пример (Задача о встрече). Предположим, что два человека условились встретиться в 00.00 часов. У каждого встречающегося часы могут ошибаться ±5 минут. В пределах от —5 до +5 любая ошибка возможна. Множество элементарных событий W можно представить в следующем виде:
W = {(X, Y): -5 £ Х £ 5, -5 £ Y £ 5},
где Х— величина ошибки (время) в часах первого человека, а Y — в часах второго человека, выраженные в минутах. Нас интересует вероятность события А = { встреча состоялась }. В зависимости от того, каковы условия договоренности этих людей, задача решается по-разному. Например, пусть они договорились о том, что каждый после прихода ждет 3 минуты. При этом встреча может состояться только тогда, когда выполнено следующее условие: ½ Х — Y ½ £ 3. Итак, событие А интерпретируется следующим образом: А = {(Х,Y): ½ Х —Y ½£ 3}. Событию А соответствует заштрихованная область на рисунке. Теперь нам остается воспользоваться определением геометрической вероятности: Р (A) = m(A)/ m(G). Элементарные вычисления показывают, что m (A) = 100 - 7 × 7 = 51, m(W) = 100, и поэтому Р (A) = 51/100.
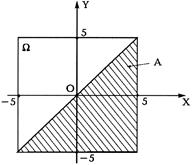 |
Теперь предположим, что они договорились о том, что первый приходит и не ждет ни секунды, а второй ждет. При этих условиях встреча может состояться только при выполнении следующего условия: Х ³ Y. Тогда событие А выглядит так: А = {(X,Y): Х ³Y}
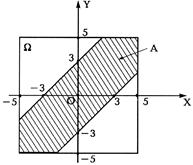 |
Воспользовавшись определением геометрической вероятности, находим P (A)=m(A)/ m(G)=1/2.
 2014-02-18
2014-02-18 448
448







