Закон больших чисел. Сходимость последовательности случайных величин по вероятности

Сходимость последовательности случайных величин по вероятности

Предельные теоремы теории вероятностей

Пусть x ₁, x ₂, …., x_n … — последовательность случайных величин.

Определение. Последовательность x ₁, x ₂, …., x_n … сходится к числу а по вероятности, если для любого e > 0 выполняется

Р (| x_n — a | ³ e) ® 0 при п ® ¥.

(т.е. lim _{п ® ¥} Р (| x_n — a | ³ e) = 0)

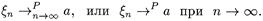Эту сходимость обозначают так:

Пусть существуют Е x_n = a_n. Рассмотрим следующую разность

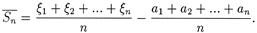Нас интересует поведение 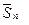при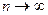

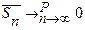Определение. Будем говорить, что последовательность случайных величин x ₁, x ₂, …., x_n … подчиняется закону больших чисел (ЗБЧ), если

Замечание. Пусть x ₁, x ₂, …., x_n — случайные величины, имеющие одинаковое распределение. Тогда a_n = а. Пусть x ₁, x ₂, …., x_n интерпретируются как измерения некоторой физической величины а. Так как точные измерения невозможны, то x ₁, x ₂, …, x_n — последовательность случайных величин, тогда ЗБЧ означает, что среднее арифметическое первых п измерений хорошо аппроксимирует а:

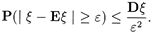Теорема 1 (неравенство Чебышева). Для любой случайной величины x, имеющей математическое ожидание (Е x < ¥), при любом e > 0 имеет место неравенство

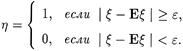Доказательство. Рассмотрим следующую случайную величину h

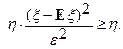Тогда

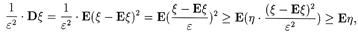поскольку

С другой стороны

E h = 1× P (êx- E x ê³ e) + 0 × P (êx- E x ê< e) = P (êx- E x ê³ e).

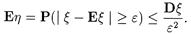Тогда получаем

Приведем несколько теорем, которые относятся к законам больших чисел.

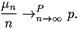Теорема 2 (Я. Бернулли). Пусть m_n — число успехов в п испытаниях Бернулли с вероятностью успеха р. Тогда

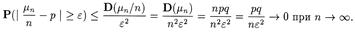Доказательство. Поскольку Е (m_n / n) = р, то неравенство Чебышева дает

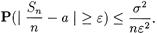Теорема 3 (Чебышева). Пусть x ₁, x ₂, …, x_n — последовательность независимых и одинаково распределенных случайных величин с Е x_i, = а и конечной дисперсией D x_i = s ², i = 1, 2,..., 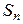= S ⁿ_{i =1} x_i. Тогда для любого e > 0 имеет место

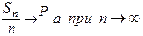В частности,

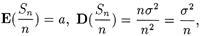Доказательство. Поскольку

то, воспользовавшись неравенством Чебышева мы получим требуемое.

Пример. Технический контролер проверяет партию однотипных приборов. С вероятностью 0,01 прибор может иметь дефект A и, независимо от этого, с вероятностью 0,02 - дефект В. В каких границах будет заключено практически наверняка число бракованных изделий в партии из 1000 штук, если за вероятность практической достоверности принимается 0,997?

Обозначим через m_п —число бракованных изделий в партии из п = 1000 штук, Е m_п = пр, где р —вероятность иметь дефекта для одного прибора:

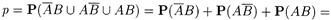0,01 × 0,98 + 0,02 × 0,99 + 0, 01 × 0,02 @ 0,03.

Отсюда,

Е m_п = 1000 × 0,03 = 30, D m_п = npq = 30 × 0,97 = 29,1.

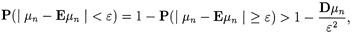Из неравенства Чебышева, получим

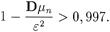и по условию задачи, правая часть этого неравенства превосходит 0,997, т.е.

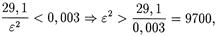Отсюда найдем e: минимальное e» 98. Тогда из | m_п — 30 | < 98 получим 0 < m_п < 128.