2014-02-18
802
Итак, пусть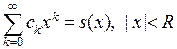 
. Положим 
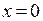, тогда получим: 
.
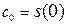Возьмем производную от членов ряда и его суммы: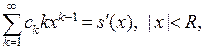 
и положим 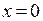. Тогда 
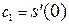. Продолжая процесс дифференцирования, получим: 
.
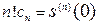То есть,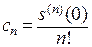 
. Таким образом, коэффициенты степенного ряда являются коэффициентами формулы Тейлора для суммы ряда.
Поставим вопросы: если для произвольной функции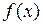 
, имеющей бесконечное число производных в точке 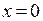построить ряд 
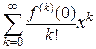, называемый рядом Тейлора функции 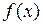, то 1) где он будет сходиться, и
2) если будет сходиться, то будет ли сходиться к самой функции?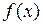
Ответы на поставленные вопросы.
1) Так как ряд Тейлора 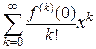– это степенной ряд, то для него обычным образом можно находить радиус и интервал сходимости. То есть, 
.
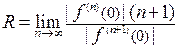2) Так как частная сумма ряда Тейлора – это полином из формулы Тейлора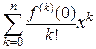 
, то разность между частной суммой и функцией 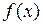согласно формуле Тейлора есть остаточный член формулы Тейлора. Мы его
рассматривали в форме Лагранжа: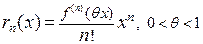 
. Таким образом, если внутри интервала сходимости остаточный член формулы
Тейлора стремится к нулю с ростом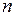 
, то сумма ряда Тейлора совпадает с
исходной функцией, по которой построен ряд. И тогда говорят, что
функция 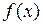представима в виде ряда Тейлора, то есть
.
