1. В соответствии с признаком Даламбера если 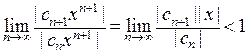 , то
, то 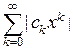 сходится, если
сходится, если 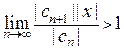 , то ряд
, то ряд 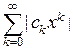 расходится. Следовательно, при
расходится. Следовательно, при 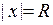 имеем:
имеем: 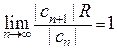 или
или 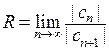 .
.
2. Аналогично используя признак Коши, получим 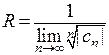 .
.
П р и м е р 1. Найти область сходимости степенного ряда 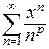 . Найдем радиус сходимости. Здесь
. Найдем радиус сходимости. Здесь 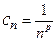 . Следовательно,
. Следовательно, 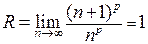 .
.
Проверим сходимость в точке 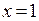 . Имеем ряд
. Имеем ряд 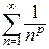 , который сходится, если
, который сходится, если 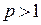 и расходится, если
и расходится, если 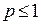 .
.
Проверим сходимость в точке 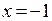 . Имеем ряд
. Имеем ряд 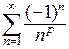 , который сходится, если
, который сходится, если 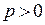 и расходится, если
и расходится, если 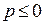 .
.
Замечание. Внутри интервала сходимости ряд можно почленно интегрировать и дифференцировать любое число раз. Это значит, что если 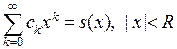 , то 1)
, то 1) 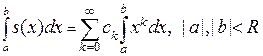 ,
,
2) 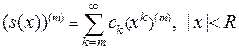 .
.
 2014-02-18
2014-02-18 378
378








