Примеры разложения функций в ряды Тейлора

Пример 1. Рассмотрим функцию 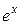. В соответствии с формулой Тейлора

,

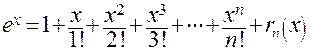где .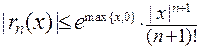

Сосчитаем радиус сходимости степенного ряда.

.

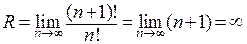Таким образом, этот ряд сходится во всех точках вещественной оси.

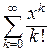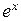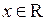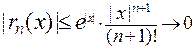Для того, чтобы выяснить, будет ли сходиться ряд к функции , заметим, что при любом значении имеем при 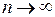. Следовательно, 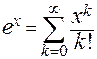при всех .

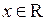Пример 2. Рассмотрим функцию 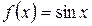. В соответствии с формулой

Тейлора

,

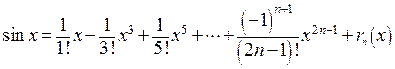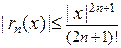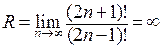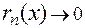где . То есть, и при 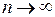. Следовательно, 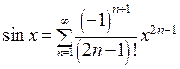при всех .

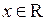Пример 3. Рассмотрим функцию 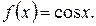В соответствии с формулой

Тейлора

,

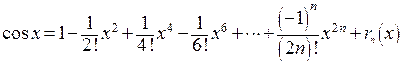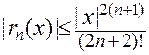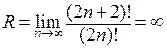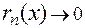где. То есть, и при 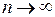. Следовательно, 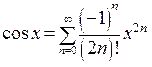при всех .

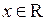Пример 4. Рассмотрим функцию 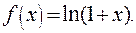В соответствии с

формулой Тейлора

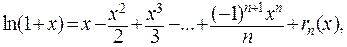
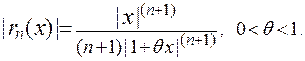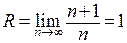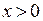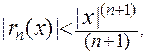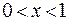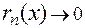где Сосчитаем радиус сходимости этого ряда: . Форма Лагранжа остаточного члена здесь годится только для . В этом случае и для имеем при 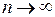. Другая форма остаточного члена для

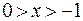приводит к подобному результату. Поэтому для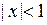

справедливо представление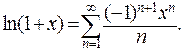

Пример 5. Рассмотрим функцию 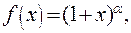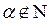. В соответствии с

формулой Тейлора .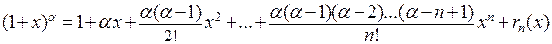

Найдем радиус сходимости этого степенного ряда: .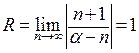

Для оценки остаточного члена при 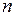, больших или равных целой части ,

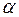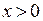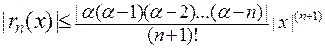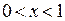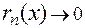форма Лагранжа остаточного члена годится также только для . В этом случае имеем оценку: . Очевидно, что при имеем при 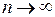. Для отрицательных значений 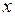применяем другую форму остаточного члена. В результате для 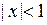справедливо представление .

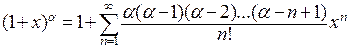Легко заметить, что полученная формула есть бесконечный аналог формулы

бинома Ньютона.